Combined benefits

Life Insurance Products Valuation in R

Roel Verbelen, Ph.D.

Statistician, Finity Consulting

Endowment insurance

Sending baby Incredible to college

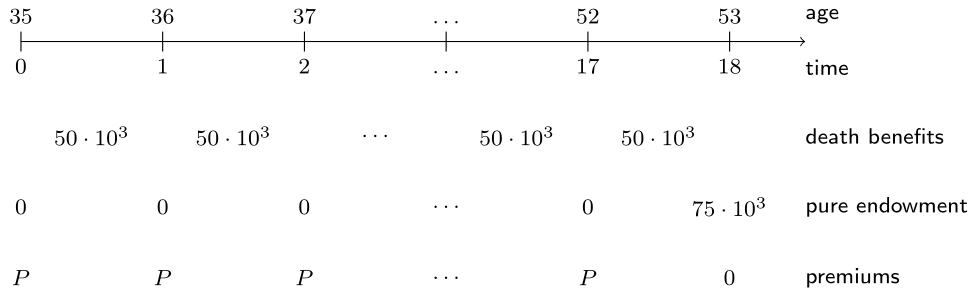
Mrs. Incredible is 35 years old.

She wants to save money to send her baby to college. She needs 75,000 EUR when he gets 18.

Given her dangerous lifestyle as a superhero, at the same time she wants to cover her life.

The sum insured is 50,000 euro.

Can you design this type of life insurance policy?

Sending baby Incredible to college pictured

Sending baby Incredible to college in R

She is 35-years-old, living in Belgium, year 2013.
Interest rate is 3%.
```
i <- 0.03
```

Death benefits (using the deferred mortality probabilities $q_{35}$, $_{1|}q_{35}$ to $_{17|}q_{35}$)

kqx <-  c(1, cumprod(px[(35 + 1):(51 + 1)])) * qx[(35 + 1):(52 + 1)]
discount_factors <- (1 + i) ^ - (1:length(kqx))
benefits <- rep(50000, length(kqx))
EPV_death_benefits <- sum(benefits * discount_factors * kqx)
EPV_death_benefits

870.8815

Sending baby Incredible to college in R

Pure endowment (using the survival probability $_{18}p_{35}$)

EPV_pure_endowment <- 75000 * (1 + i) ^ - 18 * prod(px[(35 + 1):(52 + 1)])
EPV_pure_endowment

42975.86

Premium pattern rho (using the survival probabilities $_{0}p_{35}$ to $_{17}p_{35}$)

# Premium pattern rho
kpx <- c(1, cumprod(px[(35 + 1):(51 + 1)]))
discount_factors <- (1 + i) ^ - (0:(length(kpx) - 1))
rho <- rep(1, length(kpx))
EPV_rho <- sum(rho * discount_factors * kpx)
EPV_rho

14.06193

Sending baby Incredible to college in R

Actuarial equivalence

$$ P = \frac{\text{EPV}(\text{death benefits})+\text{EPV}(\text{pure endowment})}{\text{EPV}(\text{rho})}. $$

# Premium level
(EPV_death_benefits + EPV_pure_endowment) / EPV_rho

3118.116

Let's practice!

Life Insurance Products Valuation in R