Valuation

Life Insurance Products Valuation in R

Roel Verbelen, Ph.D.

Statistician, Finity Consulting

Discount factors

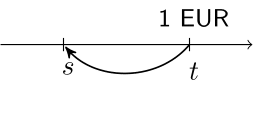
Denote: $v(s,t)$ the value at time $s$ of 1 EUR paid at time $t$.
$s < t$: a discounting factor

Discount factors

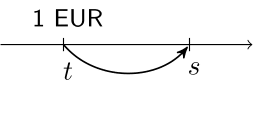
Denote: $v(s,t)$ the value at time $s$ of 1 EUR paid at time $t$.
$s > t$: an accumulation factor

Discount factors in R

i <- 0.03
v <- 1 / ( 1 + i)

With $s<t$: e.g. $s=2$ and $t=4$

s <- 2 
t <- 4

# v(2, 4) = value at time 2 of 1 EUR paid at time 4
v ^ (t - s)

0.9425959

(1 + i) ^ - (t - s)

0.9425959

Discount factors in R

i <- 0.03
v <- 1 / ( 1 + i)

With $s>t$: e.g. $s=6$ and $t=3$

s <- 6
t <- 3

# v(6, 3) = value at time 6 of 
#           1 EUR paid at time 3
v ^ (t - s)

1.092727

(1 + i) ^ - (t - s)

1.092727

Valuation of a cash flow vector

The value at time $n$

$$ \sum_{k=0}^N c_k \cdot v(n,k) $$

$\qquad$ with $0 \leq n \leq N$.

Present Value ($n=0$) and Accumulated Value ($n=N$).

Valuation of a cash flow vector in R

# Define the discount function
discount <- function(s, t, i = 0.03) {(1 + i) ^ - (t - s)}

# Calculate the value at time 3
value_3 <- 500 * discount(3, 0) + 300 * discount(3, 2) + 200 * discount(3, 7)
value_3

1033.061

Valuation of a cash flow vector in R

# Define the discount function
discount <- function(s, t, i = 0.03) {(1 + i) ^ - (t - s)}

# Define the cash flows 
cash_flows <- c(500, 0, 300, rep(0, 4), 200)

# Calculate the value at time 3
sum(cash_flows * discount(3, 0:7))

1033.061

Let's practice!

Life Insurance Products Valuation in R