Binomial experiments

Life Insurance Products Valuation in R

Roel Verbelen, Ph.D.

Statistician, Finity Consulting

The life table in R

life_table contains the period life table for males in Belgium of 2013.

head(life_table, 10)

   age      qx     lx  dx    ex
1    0 0.00381 100000 381 77.95
2    1 0.00047  99619  47 77.24
3    2 0.00019  99572  19 76.28
4    3 0.00015  99553  15 75.30
5    4 0.00013  99538  13 74.31
6    5 0.00010  99525  10 73.32
7    6 0.00011  99514  11 72.32
8    7 0.00008  99504   8 71.33
9    8 0.00011  99496  11 70.34
10   9 0.00008  99485   8 69.34

# Variables used in this video
qx <- life_table$qx
px <- 1 - qx
lx <- life_table$lx
dx <- life_table$dx

A binomial experiment: surviving one year

Focus on $\ell_x$ in life_table.

lx[0 + 1]

1e+05

A binomial experiment: surviving one year

The number of survivors up to age $x+1$ follows a BIN($\ell_x$,$\ p_{x}$).

lx[72 + 1]

px[72 + 1]

0.97369

rbinom(n = 1, size = lx[72 + 1], prob = px[72 + 1])

A binomial experiment: surviving one year

Now in a vectorized way!

sims <- rbinom(n = length(lx), size = lx, prob = px)
head(sims)

99637 99567 99553 99546 99525 99515

A binomial experiment: surviving $k$ years

The number of 1-year survivors follows a BIN($\ell_x$,$\ p_{x}$).
$\quad \,$ Expected value:
$$ \ell_{x+1} = \ell_x \cdot p_x. $$
The number of $k$-year survivors follows a BIN($\ell_x$,$\ _{k}p_{x}$).

$\quad \,$ Expected value:

$$ \ell_{x+k} = \ell_{x} \cdot \ _{k}p_{x}. $$

$\quad \,$ Thus:

$$ _{k}p_{x} = \frac{\ell_{x+k}}{\ell_{x}}. $$

A binomial experiment: the number of deaths

The number of deaths follows a BIN($\ell_x$,$\ q_{x}$).

$\quad \,$ Expected value: $$ \large \begin{aligned} d_x &= \ell_x \cdot q_x \\ &= \ell_x \cdot (1-p_x) \\ &= \ell_x -\ell_{x+1}. \end{aligned} $$

dx[72 + 1]

lx[72 + 1] - lx[73 + 1]

Survival probabilities in R

Compute $_5p_{65} = \dfrac{\ell_{70}}{\ell_{65}}$.

# Probability that (65) survives 5 more years
lx[age == 70] / lx[age == 65]

0.9143957

# Alternatively
lx[70 + 1] / lx[65 + 1]

0.9143957

Picturing survival probabilities in R

# probability that (65) survives to age 65 + k
k <- 0:45
plot(k, 
     lx[65 + k + 1] / lx[65 + 1], 
     pch = 20, 
     xlab = "k", 
     ylab = expression(paste(""[k], "p"[65])))

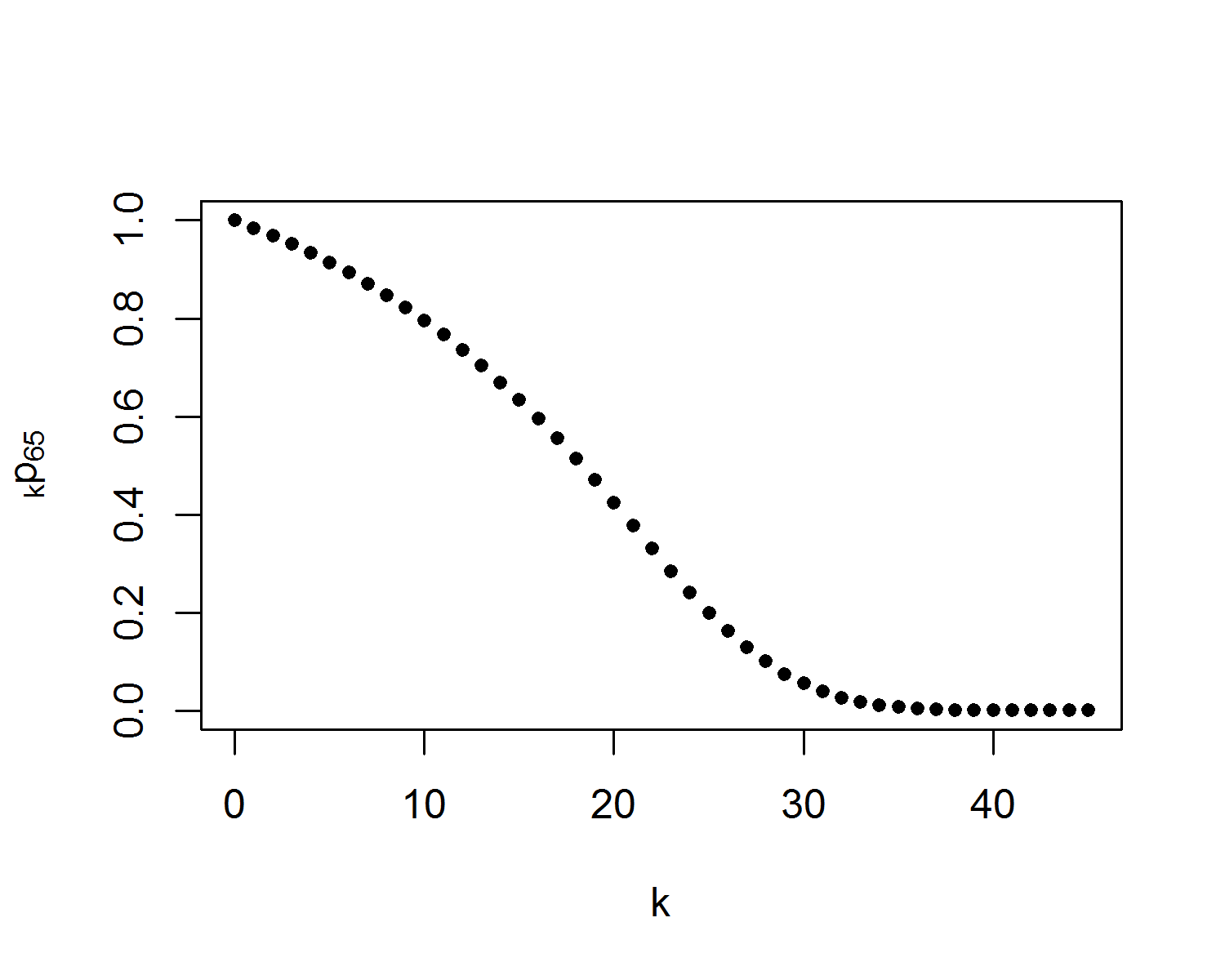
Let's practice!

Life Insurance Products Valuation in R