Calculating probabilities
Life Insurance Products Valuation in R

Katrien Antonio, Ph.D.
Professor, KU Leuven and University of Amsterdam
From one-year to multi-year survival probabilities
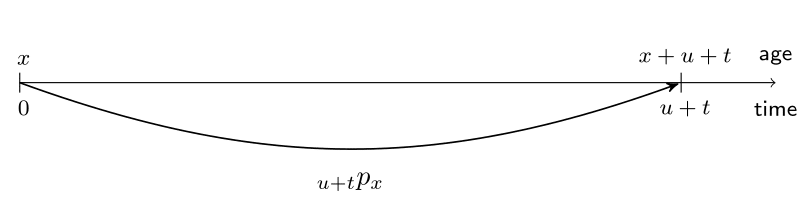
From one-year to multi-year survival probabilities
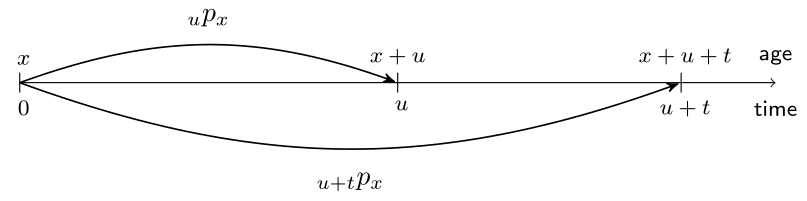
From one-year to multi-year survival probabilities
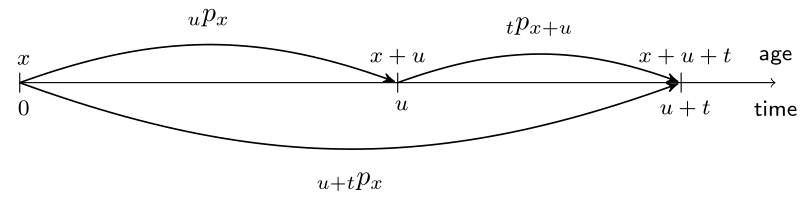
From one-year to multi-year survival probabilities
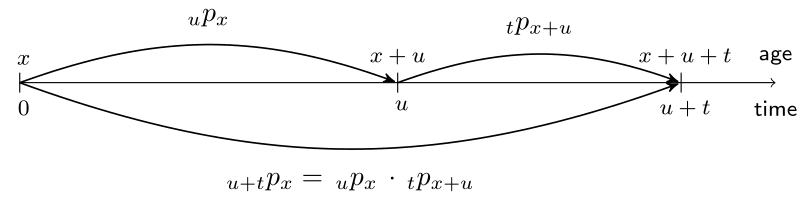
The multiplication rule
- Rewriting the survival probabilities:
$$ _{t+u}p_x =\ _{u}p_x \cdot \ _{t}p_{x+u}. $$
The multiplication rule
Rewriting the survival probabilities:
$$ _{t+u}p_x =\ _{u}p_x \cdot \ _{t}p_{x+u}. $$
With $k$ an integer we obtain:
$$ \begin{aligned} _kp_x &= p_x \cdot \ _{k-1}p_{x+1} \\ &= p_x \cdot p_{x+1} \cdots p_{x+k-1} \\ &= \prod_{l=0}^{k-1} p_{x+l} \end{aligned} $$
$\quad \,$ which is a product of one-year survival probabilities.
Calculating survival probabilities in R
Compute $_5p_{65} = p_{65} \cdot p_{66} \cdot p_{67} \cdot p_{68} \cdot p_{69}$.
# One-year survival probabilities
px <- 1 - life_table$qx
px[(65 + 1):(69 + 1)]
0.98491 0.98320 0.98295 0.98091 0.97935
# Probability that (65) survives 5 more years
prod(px[(65 + 1):(69 + 1)])
0.9144015
Compute $_5p_{65} = \frac{\ell_{70}}{\ell_{65}}$.
# Alternatively (difference due to
rounding)
lx[70 + 1] / lx[65 + 1]
0.9143957
Cumulative product of survival probabilities in R
Compute $_kp_{65}$ for $k = 1, 2, 3, 4, 5$.
# One-year survival probabilities
px[(65 + 1):(69 + 1)]
0.98491 0.98320 0.98295 0.98091 0.97935
# Multi-year survival probabilities of (65)
cumprod(px[(65 + 1):(69 + 1)])
0.9849100 0.9683635 0.9518529 0.9336820
0.9144015
Compute $_kp_{65}$ for $k = 0, 1, 2, 3, 4, 5$.
# Multi-year survival probabilities of (65)
c(1, cumprod(px[(65 + 1):(69 + 1)]))
1.0000000 0.9849100 0.9683635 0.9518529
0.9336820 0.9144015
A deferred mortality probability
- Focus on a specific deferred mortality probability:
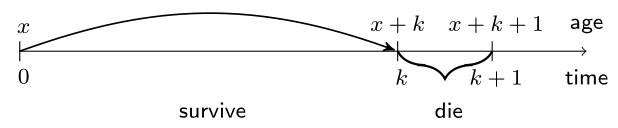
- $(x)$ survives $k$ whole years, but dies before reaching age $x + k + 1$:
$$ \begin{aligned} _{k|}q_x &= {}_kp_x \cdot q_{x+k}. \end{aligned} $$
A deferred mortality probability in R
Compute $_{5|}q_{65} = {}_5p_{65} \cdot q_{70}$.
# 5-year deferred mortality probability of (65)
prod(px[(65 + 1):(69 + 1)]) * qx[70 + 1]
0.02086664
Compute $_{5|}q_{65} = \frac{d_{70}}{\ell_{65}}$.
# Alternatively (difference due to rounding)
dx[70 + 1] / lx[65 + 1]
0.02086817
Deferred mortality probabilities in R
Compute $_{k|}q_{65} = {}_kp_{65} \cdot q_{65 + k}$ for $k = 0, 1, 2, \ldots$
# Survival probabilities of (65)
kpx <- c(1, cumprod(px[(65 + 1):(length(px) - 1)]))
head(kpx)
1.0000000 0.9849100 0.9683635 0.9518529 0.9336820 0.9144015
# Deferred mortality probabilities of (65)
kqx <- kpx * qx[(65 + 1):length(qx)]
head(kpx)
0.01509000 0.01654649 0.01651060 0.01817087 0.01928053 0.02086664
Let's practice!
Life Insurance Products Valuation in R

