The whole, temporary and deferred life insurance

Life Insurance Products Valuation in R

Katrien Antonio, Ph.D.

Professor, KU Leuven and University of Amsterdam

A series of one-year contracts

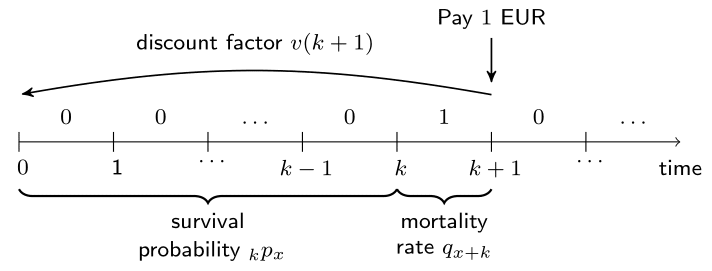
What if?
- The benefit is $b_k$ EUR instead of 1 EUR?
- A series of one-year contracts instead of just one?

General setting

A life insurance on $(x)$ with death benefit vector

$$ (b_0,b_1, \ldots, b_k, \ldots) $$
Series of one-year contracts:
- Each with $ b_k \cdot v(k+1) \cdot {}_{k}p_x \cdot q_{x+k} $ as Expected Present Value (EPV)
- Together:

$$ \sum_{k=0}^{+\infty} b_k \cdot v(k+1) \cdot {}_kp_x \cdot q_{x+k} = \sum_{k=0}^{+\infty} b_k \cdot v(k+1) \cdot {}_{k|}q_{x}$$

$\quad \, \quad \,$ the EPV.

Whole life insurance

Whole life insurance: lifelong.

Temporary life insurance

Temporary (or: term) life insurance: maximum of $n$ years.

Deferred whole life insurance

Deferred whole life insurance: no payments in first $u$ years.

Life insurances in R

Compute $A_{35}$ for constant interest rate $i = 3\%$.

# Whole-life insurance of (35)
kpx <- c(1, cumprod(px[(35 + 1):(length(px) - 1)]))
kqx <-  kpx * qx[(35 + 1):length(qx)]
discount_factors <- (1 + 0.03) ^ - (1:length(kqx))
benefits <- rep(1, length(kqx))
sum(benefits * discount_factors * kqx)

0.2880872

Now do ${}_{20|}A_{35}$.

# Deferred whole-life insurance of (35)
kpx <- c(1, cumprod(px[(35 + 1):(length(px) - 1)]))
kqx <-  kpx * qx[(35 + 1):length(qx)]
discount_factors <- (1 + 0.03) ^ - (1:length(kqx))
benefits <- c(rep(0, 20), rep(1, length(kqx) - 20))
sum(benefits * discount_factors * kqx)

0.2552956

Let's practice!

Life Insurance Products Valuation in R