Cash flows and discounting

Life Insurance Products Valuation in R

Katrien Antonio, Ph.D.

Professor, KU Leuven and University of Amsterdam

A cash flow

Fix a capital unit and a time unit:
- 0 is the present moment;
- $k$ is $k$ time units in the future (e.g. years, months, quarters).
Amount of money received or paid out at time $k$:
- $c_k$
- the cash flow at time $k$.

A vector of cash flows in R

In R:

# Define the cash flows
cash_flows <- c(500, 400, 300, rep(200, 5))
length(cash_flows)

In general: for a cashflow vector $(c_0,c_1,\ldots,c_N)$:

Valuation of a cash flow vector

Crucial facts:
- timing of cash flows matters!
- time value of money matters!
Interest rate determines growth of money.

Interest rate and discount factor

Accumulation

$i$ is the constant interest rate.

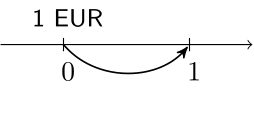
i <- 0.03
1 * (1 + i)

1.03

Discounting

$v=\displaystyle \frac{1}{1+i}$ the discount factor.

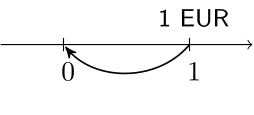
v <- 1 / (1 + i)
v

0.9708738

From one time period to k time periods

Accumulation
- the value at time $k$ of $1$ EUR paid at time $0$ $=(1+i)^k = v^{-k}$.

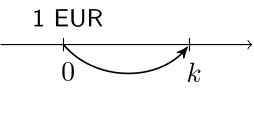
i <- 0.03 ; v <- 1 / (1 + i) ; k <- 2
c((1 + i) ^ k, v  ^ -k)

1.0609 1.0609

Discounting
- the value at time $0$ of $1$ EUR paid at time $k$ $=(1+i)^{-k} = v^{k}$.

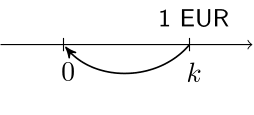
i <- 0.03 ; v <- 1 / (1 + i) ; k <- 2
c((1 + i) ^ -k, v  ^ k)

0.9425959 0.9425959

The present value of a cash flow vector

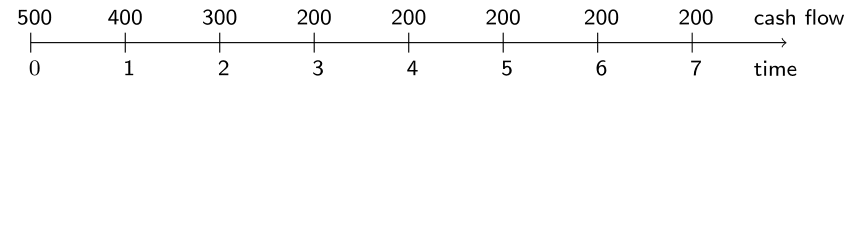
What is the value at $k=0$ of this cash flow vector?

The present value of a cash flow vector

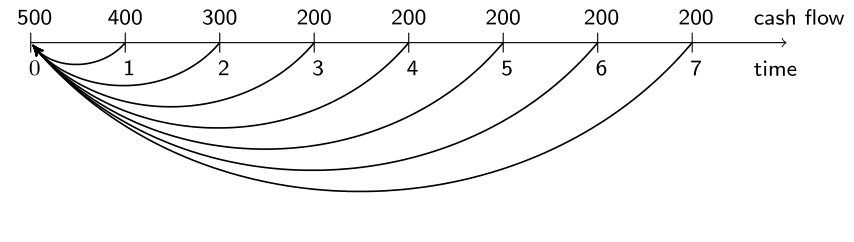
What is the value at $k=0$ of this cash flow vector?

The present value (PV)!

The present value of a cash flow vector in R

# Interest rate
i <- 0.03

# Discount factor
v <- 1 / (1 + i)

# Define the discount factors
discount_factors <- v ^ (0:7)

# Cash flow vector
cash_flows <- 
    c(500, 400, 300, rep(200, 5))

# Discounting cash flows
cash_flows * discount_factors

500.0000 388.3495 282.7788 183.0283 
177.6974 172.5218 167.4969 162.6183

# Present value of cash flow vector
present_value <- 
    sum(cash_flows * discount_factors)
present_value

[1] 2034.491

Let's practice!

Life Insurance Products Valuation in R