Adding two random variables together
Foundations of Probability in R

David Robinson
Chief Data Scientist, DataCamp
Adding two random variables
$$X \sim \text{Binom}(10, .5)$$
$$Y \sim \text{Binom}(100, .2)$$
$$Z \sim X + Y$$
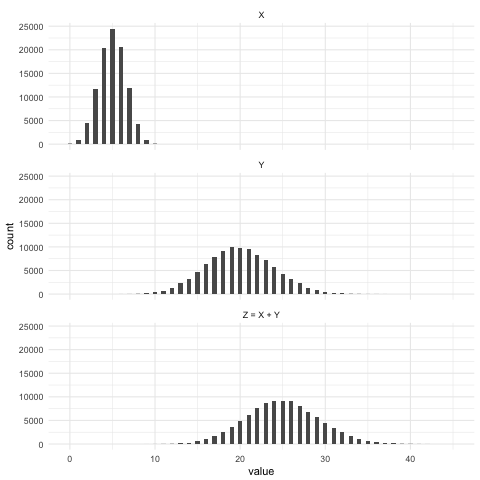
Simulation: expected value of X + Y
X <- rbinom(100000, 10, .5)
mean(X)
# [1] 5.00938
Y <- rbinom(100000, 100, .2)
mean(Y)
# [1] 19.99422
Z <- X + Y
mean(Z)
# [1] 25.0036
$$E[X+Y]=E[X]+E[Y]$$

Simulation: variance of X + Y
X <- rbinom(100000, 10, .5)
var(X)
# [1] 2.500895
Y <- rbinom(100000, 100, .2)
var(Y)
# [1] 16.06289
Z <- X + Y
var(Z)
# [1] 18.58055
$$\text{Var}[X+Y]=\text{Var}[X]+\text{Var}[Y]$$

Rules for combining random variables
$$E[X+Y]=E[X]+E[Y]$$
$$\text{ (Even if X and Y aren't independent)}$$
$$\text{Var}[X+Y]=\text{Var}[X]+\text{Var}[Y]$$
$$\text{ (Only if X and Y are independent)}$$
Let's practice!
Foundations of Probability in R

