Bayes' theorem

Foundations of Probability in R

David Robinson

Chief Data Scientist, DataCamp

Probabilities

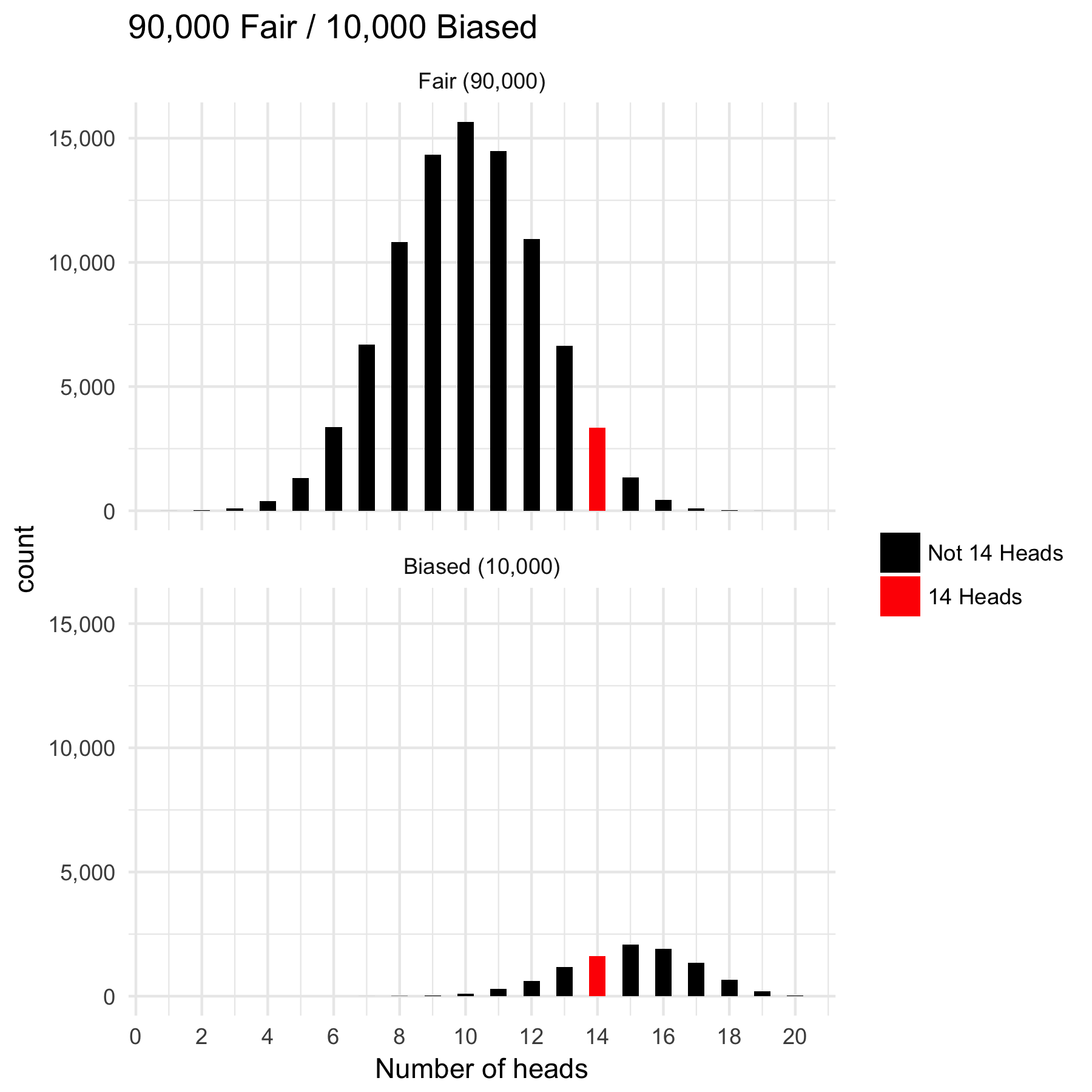
Probability of fair coin with 14 heads

fair <- rbinom(90000, 20, .5)
sum(fair == 14)
# [1] 3410

dbinom(14, 20, .5) * .9
# [1] 0.03326797

$$\Pr(\text{14 Heads}|\text{Fair})\cdot\Pr(\text{Fair})$$

biased <- rbinom(10000, 20, .75)
sum(biased == 14)
# [1] 1706

dbinom(14, 20, .75)  * .1
# [1] 0.01686093

$$\Pr(\text{14 Heads}|\text{Biased})\cdot\Pr(\text{Biased})$$

Conditional probability

$$\Pr(\text{Biased}|\text{14 Heads})=\frac{\Pr(\text{14 Heads and Biased})}{\Pr(\text{14 Heads and Biased})+\Pr(\text{14 Heads and Fair})}$$

$$=\frac{\Pr(\text{14 Heads}|\text{Biased})\Pr(\text{Biased})}{\Pr(\text{14 Heads}|\text{Biased})\Pr(\text{Biased}) + \Pr(\text{14 Heads}|\text{Fair})\Pr(\text{Fair})}$$

prob_14_fair <- dbinom(14, 20, .5) * .9
prob_14_biased <- dbinom(14, 20, .75) * .1

prob_14_biased / (prob_14_fair + prob_14_biased)

Bayes' Theorem

$$\Pr(A|B)=\frac{\Pr(B|A)\Pr(A)}{\Pr(B|A)\Pr(A) + \Pr(B|\text{not }A)\Pr(\text{not }A)}$$

$$A = \text{Biased}$$

$$B = \text{14 Heads}$$

Let's practice!

Foundations of Probability in R