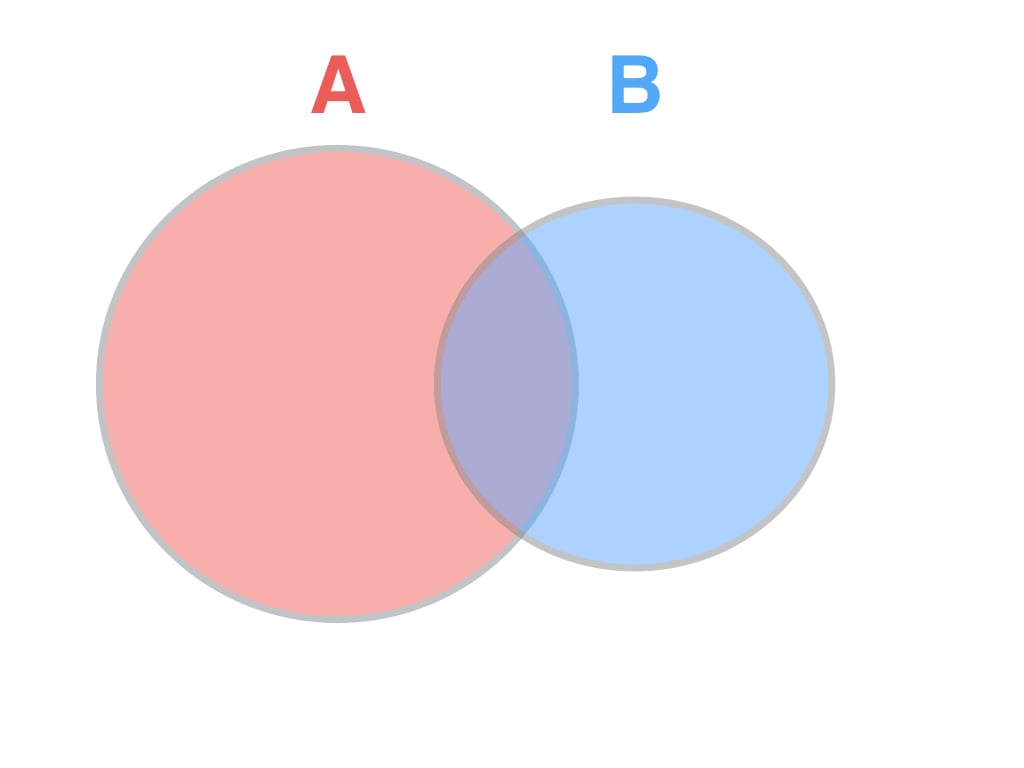
$$\Pr(A\text{ or }B)=\Pr(A)+\Pr(B)-\Pr(A\text{ and }B)$$
$$\Pr(A\text{ or }B)=\Pr(A)+\Pr(B)-\Pr(A)\cdot\Pr(B)$$
$$\Pr(A\text{ or }B)=.5+.5-.5\cdot .5=.75$$
Simulating two events
A <- rbinom(100000, 1, .5)
B <- rbinom(100000, 1, .5)
mean(A | B)
[1] 0.75125
$$\begin{aligned}\Pr(A \text{ or } B) &= \Pr(A) + \Pr(B) \\ &\phantom{=} - \Pr(A\text{ and }B) \end{aligned}$$
$$.75=.5 + .5 - .5 \cdot .5$$
A <- rbinom(100000, 1, .2)
B <- rbinom(100000, 1, .6)
mean(A | B)
[1] 0.6803
$$\begin{aligned}\Pr(A \text{ or } B) &= \Pr(A) + \Pr(B) \\ &\phantom{=} - \Pr(A\text{ and }B) \end{aligned}$$
$$.68=.2 + .6 - .2 \cdot .6$$
Three coins
$$\Pr(A\text{ or }B\text{ or }C)$$
$$=\Pr(A)+\Pr(B)+\Pr(C) -$$
$$\Pr(A\text{ and }B)-\Pr(A\text{ and }C)-\Pr(A\text{ and }B)+$$
$$\Pr(A\text{ and }B\text{ and }C)$$
Preparing Video For Download...
