The normal distribution
Foundations of Probability in R

David Robinson
Chief Data Scientist, DataCamp
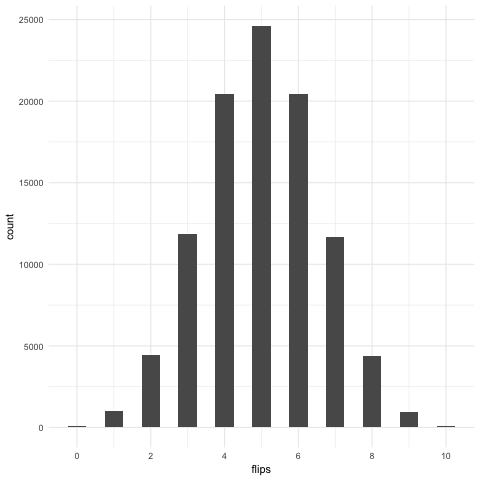
Flipping 10 coins
flips <- rbinom(100000, 10, .5)
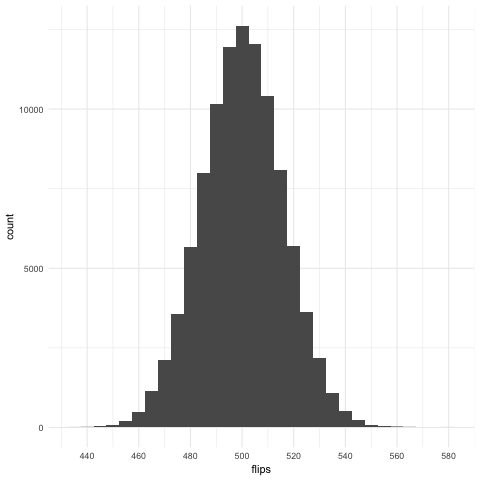
Flipping 1000 coins
flips <- rbinom(100000, 1000, .5)
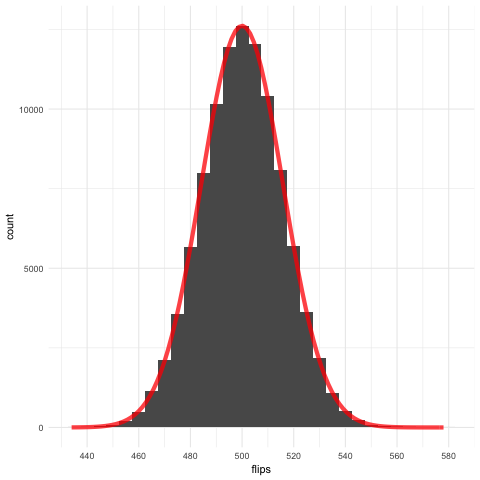
Flipping 1000 coins
Normal distribution has mean and standard deviation
$$X \sim \text{Normal}(\mu,\sigma)$$
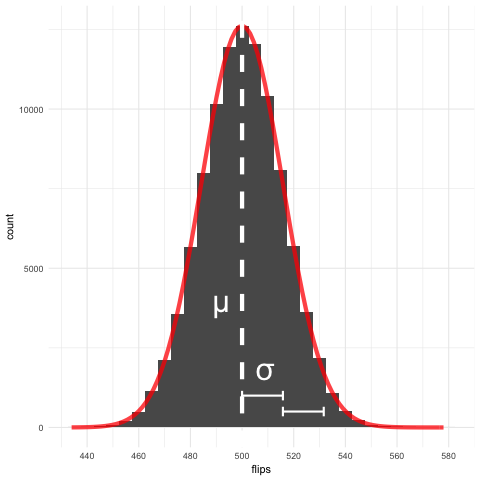
$$\sigma = \sqrt{\text{Var}(X)}$$
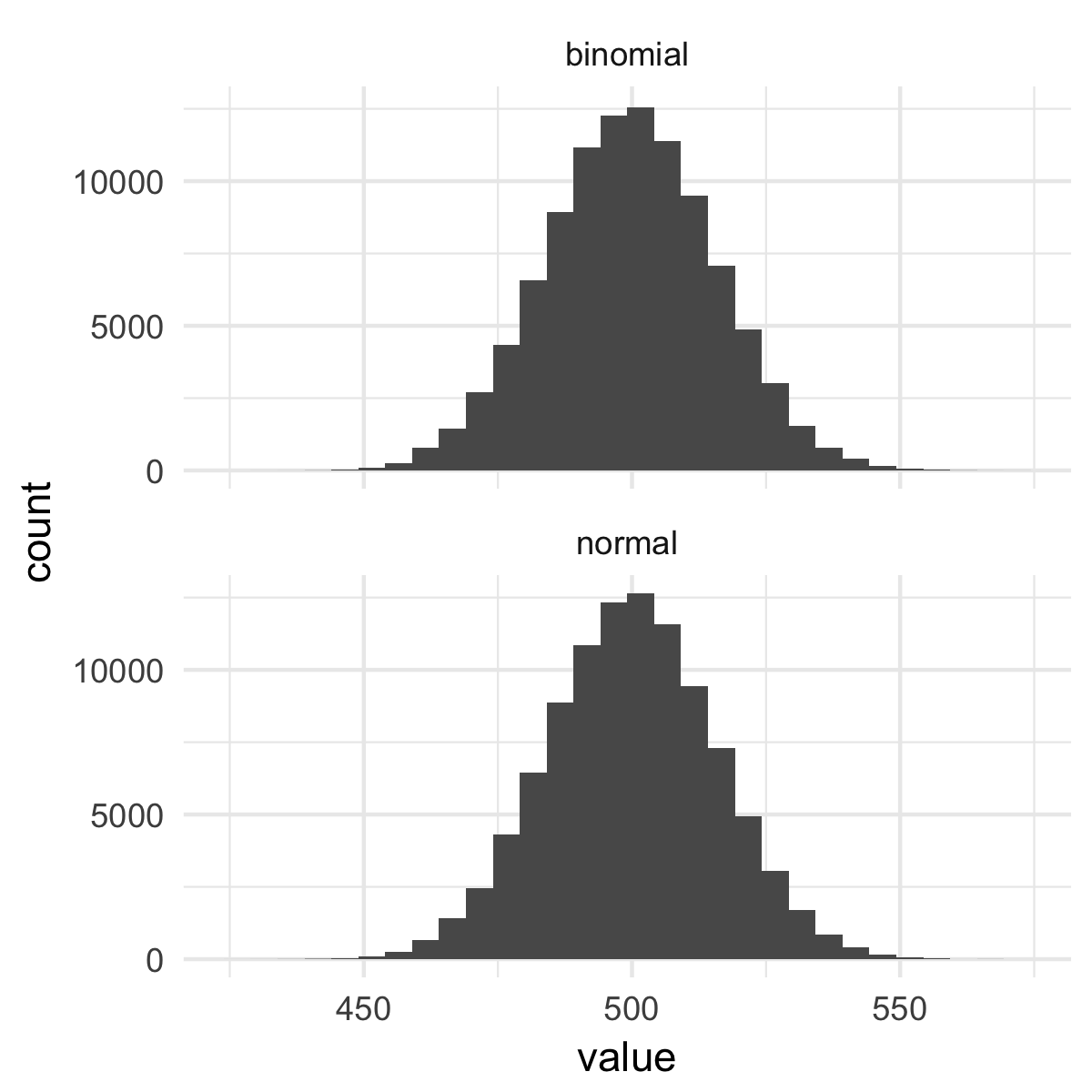
Normal approximation to the binomial
binomial <- rbinom(100000, 1000, .5)
$$\mu = \text{size} \cdot p$$ $$\sigma = \sqrt{\text{size} \cdot p \cdot (1 - p)}$$
expected_value <- 1000 * .5
variance <- 1000 * .5 * (1 - .5)
stdev <- sqrt(variance)
normal <- rnorm(100000, expected_value, stdev)
Comparing histograms
compare_histograms(binomial, normal)
Let's practice!
Foundations of Probability in R

