Multiplying random variables
Foundations of Probability in R

David Robinson
Chief Data Scientist, DataCamp
Multiplying a random variable
$$X \sim \text{Binomial}(10, .5)$$
$$Y \sim 3 \cdot X$$
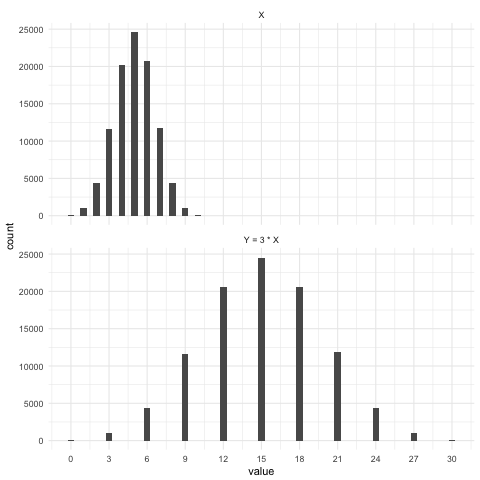
Simulation: Effect of multiplying on expected value
$$X \sim \text{Binom}(10, .5)$$
$$Y=3\cdot X$$
X <- rbinom(100000, 10, .5)
mean(X)
# [1] 5.006753
Y <- 3 * X
mean(Y)
# [1] 15.02026
$$E[k \cdot X]=k \cdot E[X]$$
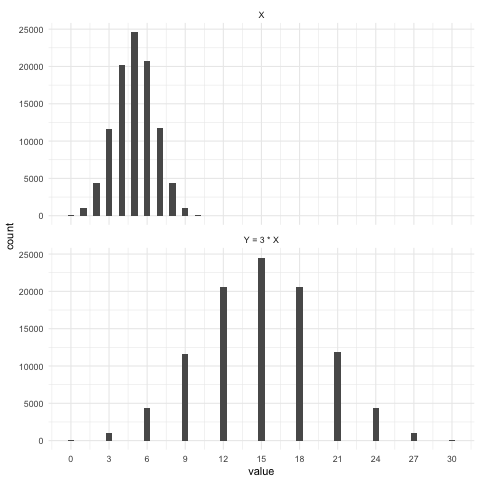
Simulation: Effect of multiplying on variance
$$X \sim \text{Binom}(10, .5)$$
$$Y=3\cdot X$$
X <- rbinom(100000, 10, .5)
var(X)
# [1] 2.500388
Y <- 3 * X
var(Y)
# [1] 22.50349
$$\text{Var}[k \cdot X]=k^2 \cdot \text{Var}[X]$$

Rules of manipulating random variables
$$E[k\cdot X] = k \cdot E[X]$$
$$\text{Var}(k \cdot Y) = k^2 \cdot \text{Var}(X)$$
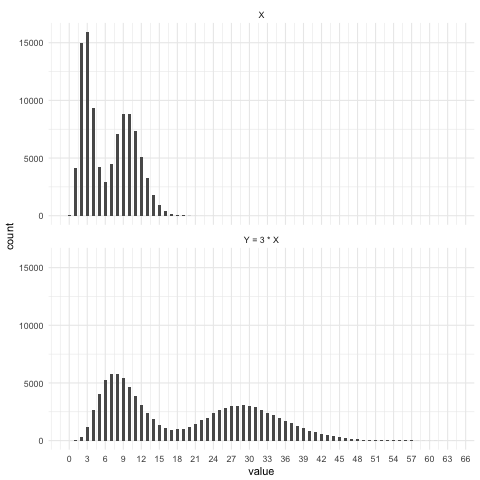
Let's practice!
Foundations of Probability in R

