Probability of event A and event B

Foundations of Probability in R

David Robinson

Chief Data Scientist, DataCamp

Event A: "Coin is heads"

A = 1

A = 0

A = 1

A = 0

B = 1

B = 0

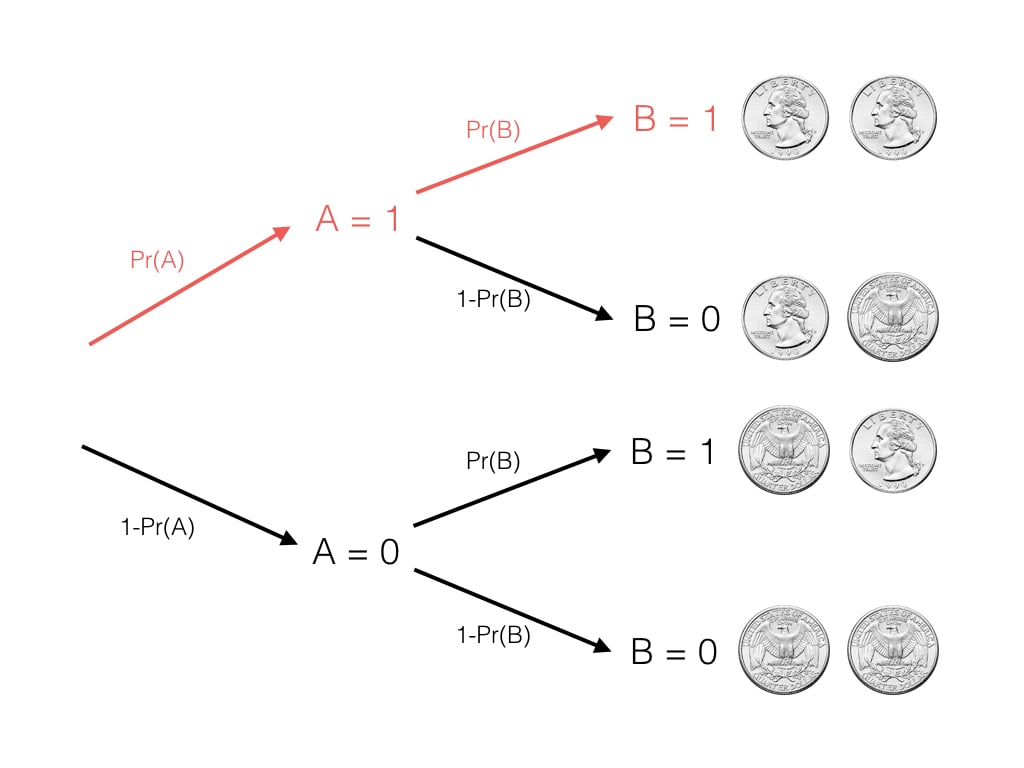
$$\Pr(A \text{ and } B) = \Pr(A) \cdot \Pr(B)$$

A <- rbinom(100000, 1, .5)

B <- rbinom(100000, 1, .5)

A & B
# [1]  FALSE TRUE FALSE  FALSE...

mean(A & B)
[1] 0.24959

$$\Pr(A \text{ and } B)=\Pr(A) \cdot \Pr(B)$$

$$\Pr(A \text{ and } B)=.5 \cdot .5=.25$$

A <- rbinom(100000, 1, .1)

B <- rbinom(100000, 1, .7)

A & B
# [1]  FALSE FALSE FALSE  FALSE...

mean(A & B)
[1] 0.07043

$$\Pr(A \text{ and } B)=\Pr(A) \cdot \Pr(B)$$

$$\Pr(A \text{ and } B)=.1 \cdot .7=.07$$

Foundations of Probability in R