Expected value and variance
Foundations of Probability in R

David Robinson
Chief Data Scientist, DataCamp
Properties of a distribution
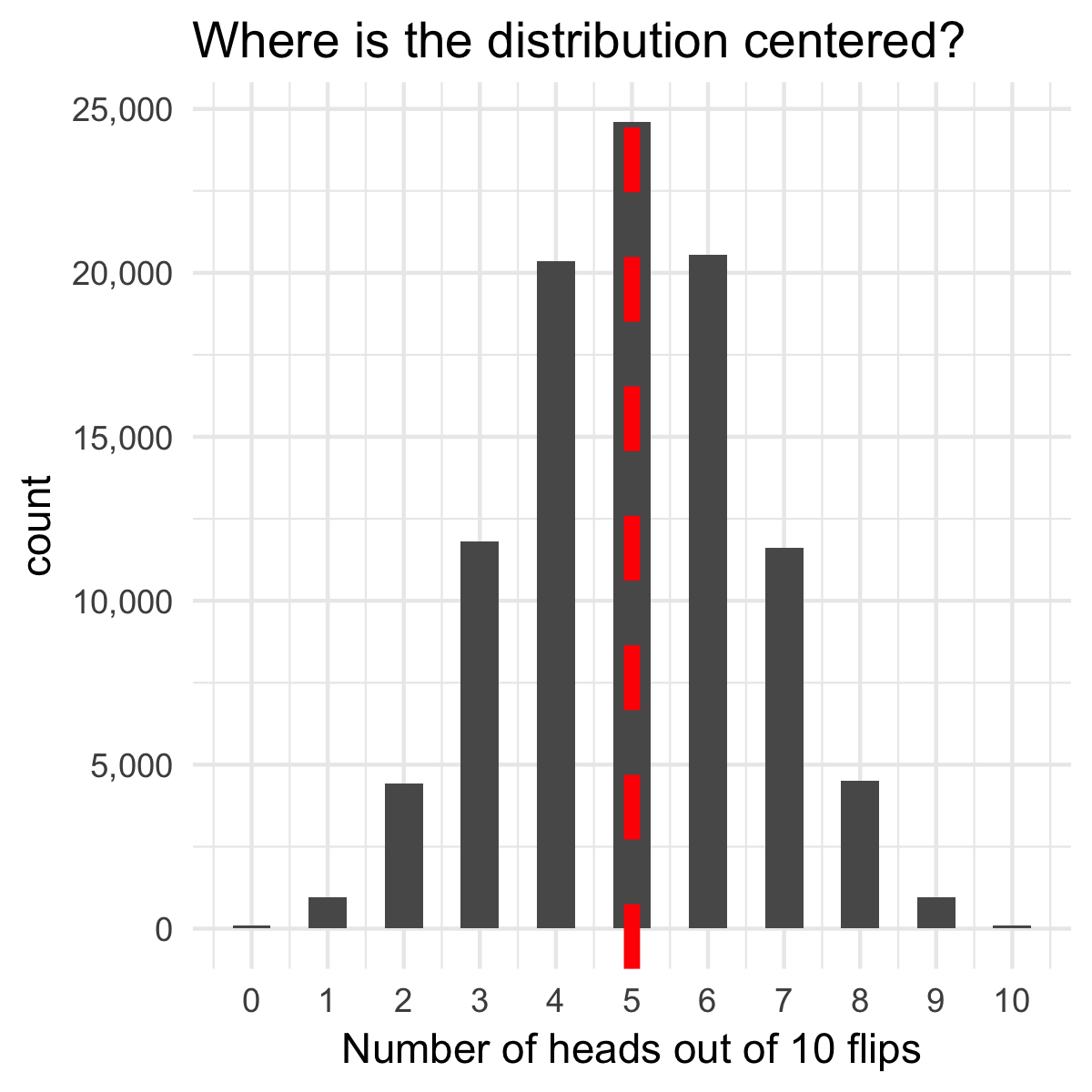
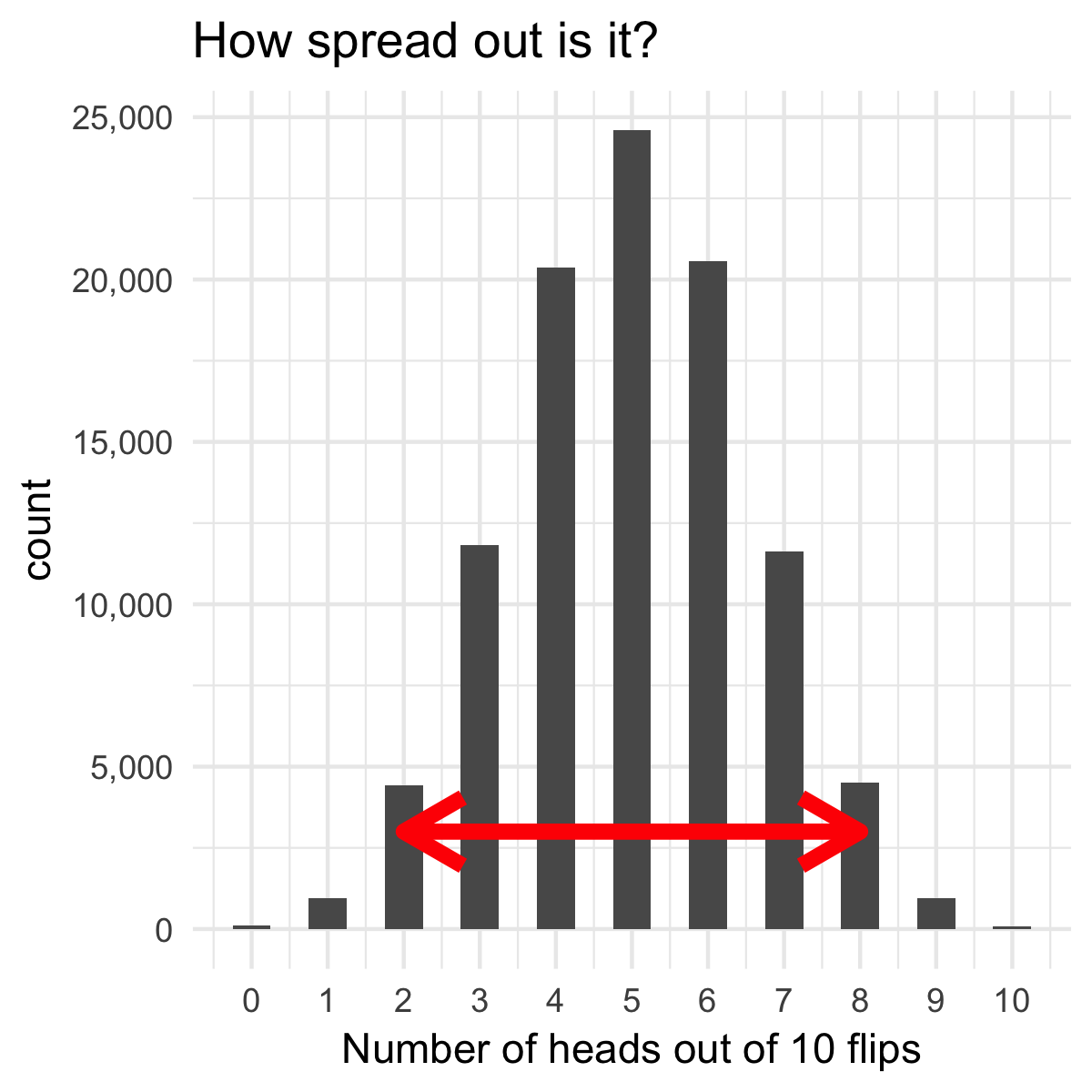
Expected value
$$X\sim \text{Binomial}(\text{size},p)$$
$$E[X]=\text{size} \cdot p$$
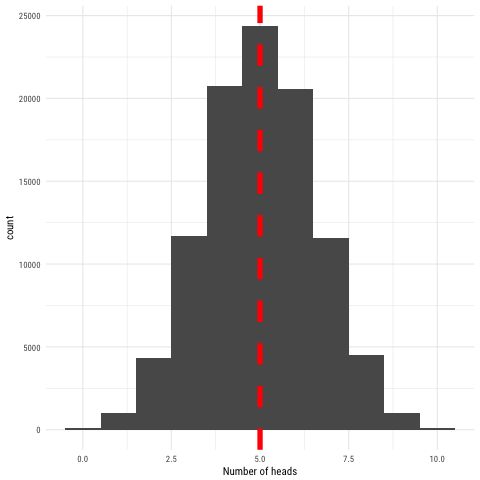
flips <- rbinom(100000, 10, .5)
mean(flips)
# [1] 5.00196
mean(rbinom(100000, 100, .2))
# [1] 19.99053
Variance
$$X\sim \text{Binomial}(10, .5)$$
X <- rbinom(100000, 10, .5)
var(X)
# [1] 2.503735
$$\text{Var}(X)=\text{size} \cdot p \cdot (1 - p)$$
$$\text{Var}(X)=10\cdot .5 \cdot (1-.5)$$ $$=2.5\enspace\enspace\enspace$$
$$Y\sim \text{Binomial}(100, .2)$$
Y <- rbinom(100000, 100, .2)
var(Y)
# [1] 16.05621
$$\text{Var}(Y)=\text{size} \cdot p \cdot (1 - p)$$
$$\text{Var}(Y)=100 \cdot .2 \cdot (1 - .2)$$ $$=16$$
Rules for expected value and variance
$$X\sim \text{Binomial}(\text{size},p)$$
$$E[X]=\text{size} \cdot p$$
$$\text{Var}(X)=\text{size} \cdot p \cdot (1 - p)$$
Let's practice!
Foundations of Probability in R

