The binomial distribution

Introduction to Statistics in R

Maggie Matsui

Content Developer, DataCamp

Coin flipping

Hand flipping coin with one side H with 50% chance, other side T with 50% chance

Binary outcomes

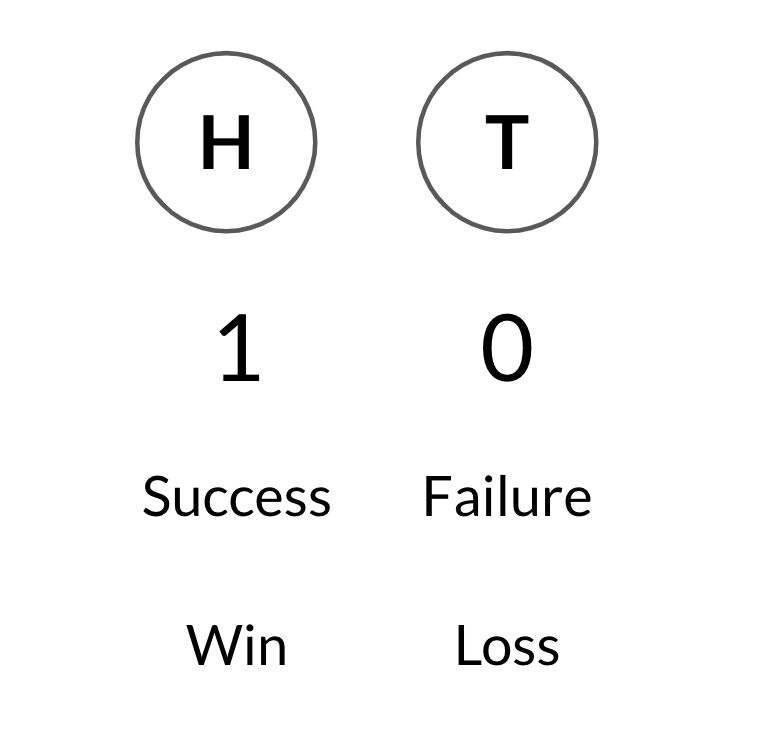
H and T, 1 and 0, Success and Failure, Win and Loss

A single flip

rbinom(# of trials, # of coins, # probability of heads/success)

1 = head, 0 = tails

rbinom(1, 1, 0.5)

rbinom(1, 1, 0.5)

One flip many times

rbinom(8, 1, 0.5)

1 0 0 1 0 0 1 0

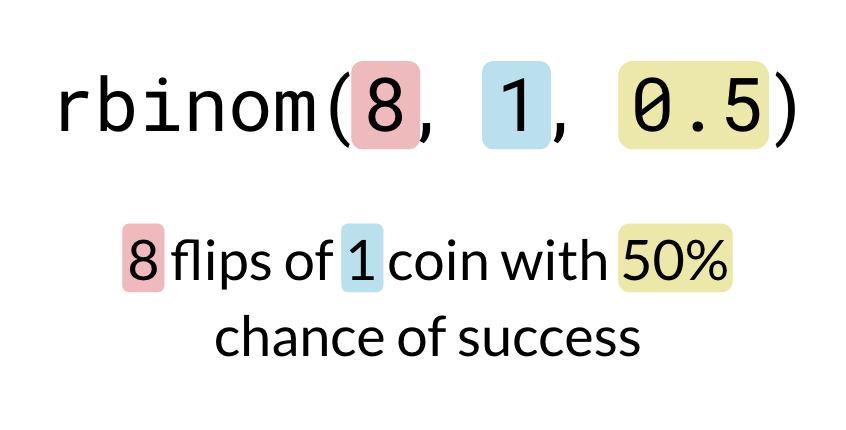
rbinom(8, 1, 0.5) with 8 in red, 1, in blue, 0.5 in yellow. Text: 8 (in red) flips of 1 (in blue) coin with 50% (in yellow) chance of success

Many flips one time

rbinom(1, 8, 0.5)

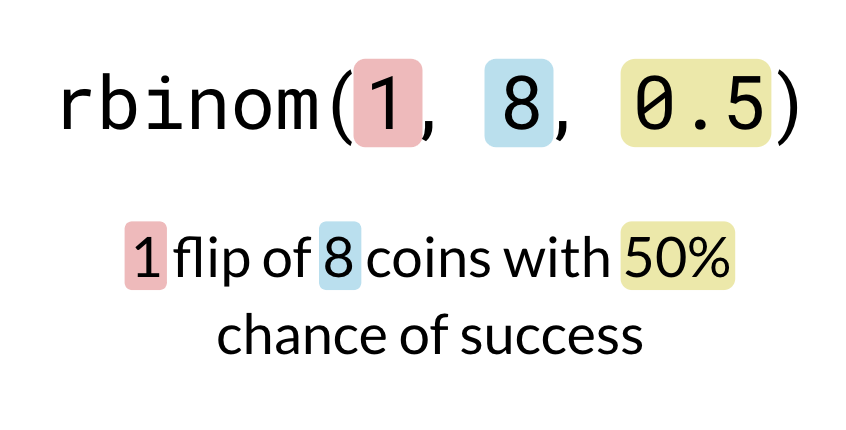
rbinom(1, 8, 0.5) with 1 in red, 8, in blue, 0.5 in yellow. Text: 1 (in red) flip of 8 (in blue) coins with 50% (in yellow) chance of success

Many flips many times

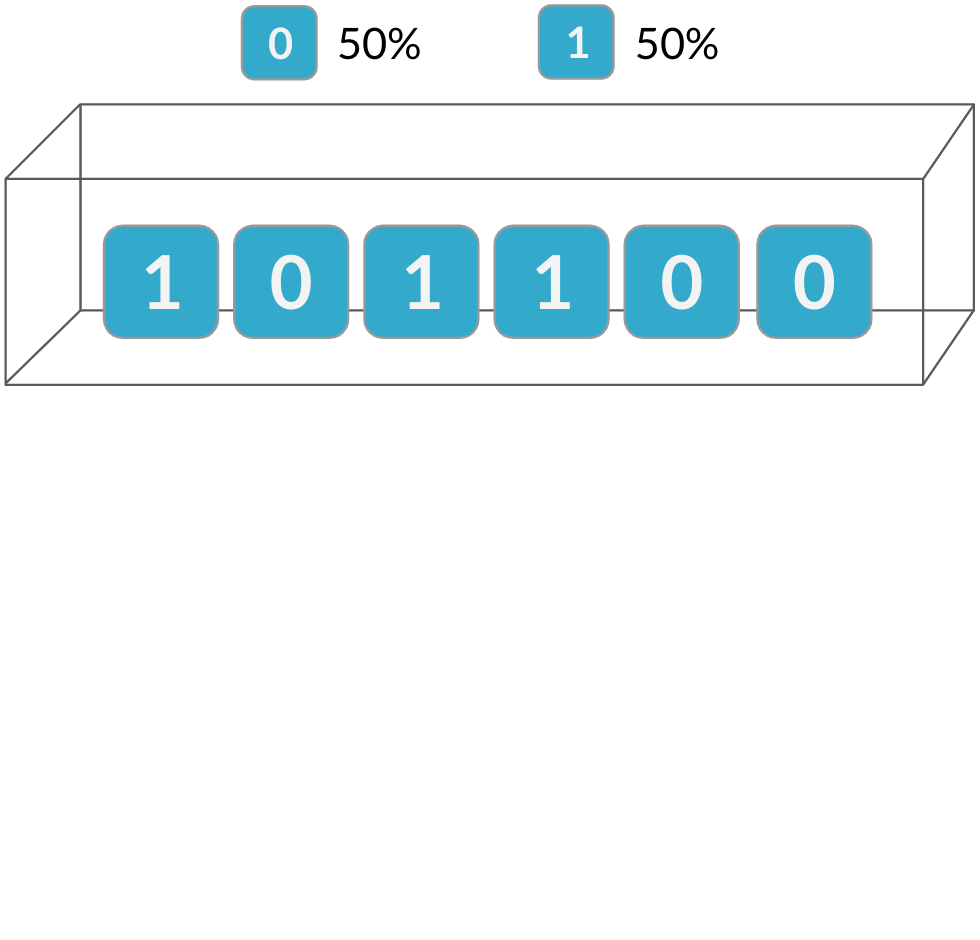
rbinom(10, 3, 0.5)

2 0 1 0 1 1 3 3 3 1

rbinom(10, 3, 0.5) with 10 in red, 3, in blue, 0.5 in yellow. Text: 10 (in red) flips of 3 (in blue) coins with 50% (in yellow) chance of success

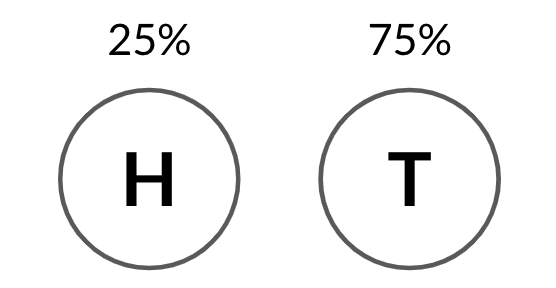
Other probabilities

rbinom(10, 3, 0.25)

1 1 0 0 1 1 1 1 2 1

Picture of heads with 25% probability and tails with 75% probability

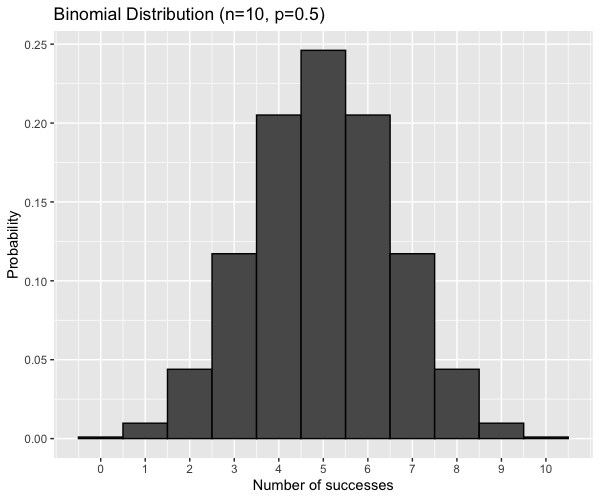
Binomial distribution

Probability distribution of the number of successes in a sequence of independent trials

E.g. Number of heads in a sequence of coin flips

Described by $n$ and $p$

$n$: total number of trials
$p$: probability of success

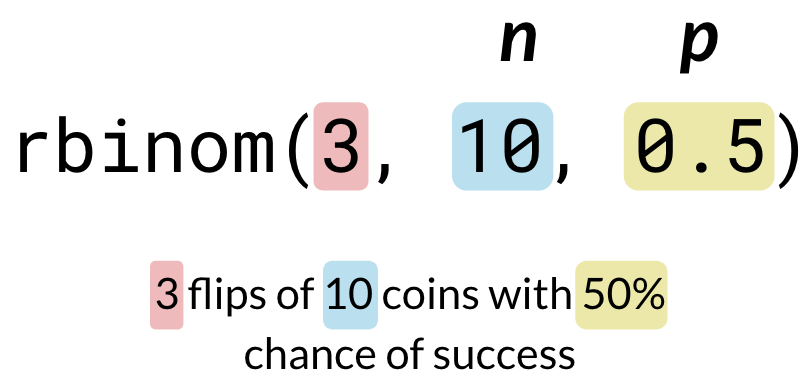
rbinom(3, 10, 0.5) with 3 in red, 10, in blue, 0.5 in yellow. Text: 3 (in red) flips of 10 (in blue) coins with 50% (in yellow) chance of success. n is written over the 10 in blue and p is written over the 0.5 in yellow.

Plot of binomial distribution with n=10, p = 0.5

What's the probability of 7 heads?

$P(\text{heads} = 7)$

# dbinom(num heads, num trials, prob of heads)
dbinom(7, 10, 0.5)

0.1171875

What's the probability of 7 or fewer heads?

$P(\text{heads} \le 7)$

pbinom(7, 10, 0.5)

0.9453125

What's the probability of more than 7 heads?

$P(\text{heads} > 7)$

pbinom(7, 10, 0.5, lower.tail = FALSE)

0.0546875

1 - pbinom(7, 10, 0.5)

0.0546875

Expected value

$\text{Expected value} = n \times p$

Expected number of heads out of 10 flips $= 10 \times 0.5 = 5$

Independence

The binomial distribution is a probability distribution of the number of successes in a sequence of independent trials

Box of tickets with 3 zeros and 3 ones. 50% chance of 0, 50% chance of 1

Independence

The binomial distribution is a probability distribution of the number of successes in a sequence of independent trials

Probabilities of second trial are altered due to outcome of the first

If trials are not independent, the binomial distribution does not apply!

Box of tickets with 3 zeros and 2 ones. 60% chance of 0, 40% chance of 1

Let's practice!

Introduction to Statistics in R