ANOVA tests

Hypothesis Testing in R

Richie Cotton

Data Evangelist at DataCamp

Job satisfaction: 5 categories

stack_overflow %>% 
  count(job_sat)

# A tibble: 5 x 2
  job_sat                   n
  <fct>                 <int>
1 Very dissatisfied       187
2 Slightly dissatisfied   385
3 Neither                 245
4 Slightly satisfied      777
5 Very satisfied          981

Visualizing multiple distributions

Question: Is mean annual compensation different for different levels of job satisfaction?

stack_overflow %>% 
  ggplot(aes(x = job_sat, y = converted_comp)) +
  geom_boxplot() +
  coord_flip()

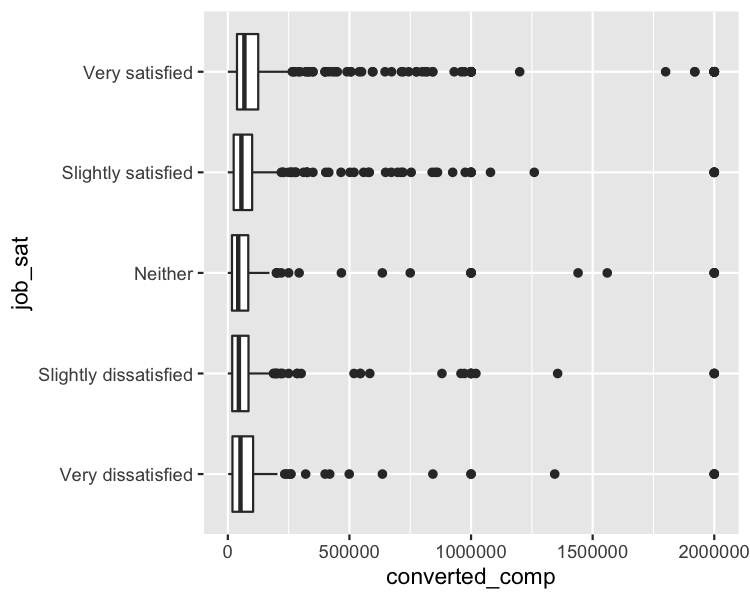
Box plot showing distribution of compensation for each of the 5 categories. "Very satisfied" looks a bit higher than the other categories, but it's difficult to tell.

Analysis of variance (ANOVA)

mdl_comp_vs_job_sat <- lm(converted_comp ~ job_sat, data = stack_overflow)

anova(mdl_comp_vs_job_sat)

Analysis of Variance Table

Response: converted_comp
            Df   Sum Sq  Mean Sq F value Pr(>F)   
job_sat      4 1.09e+12 2.73e+11    3.65 0.0057 **
Residuals 2570 1.92e+14 7.47e+10                  

Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

¹ Linear regressions with lm() are taught in "Introduction to Regression in R"

Pairwise tests

$\mu_{\text{very dissatisfied}} \neq \mu_{\text{slightly dissatisfied}}$
$\mu_{\text{very dissatisfied}} \neq \mu_{\text{neither}}$
$\mu_{\text{very dissatisfied}} \neq \mu_{\text{slightly satisfied}}$
$\mu_{\text{very dissatisfied}} \neq \mu_{\text{very satisfied}}$
$\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{neither}}$

$\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{slightly satisfied}}$
$\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{very satisfied}}$
$\mu_{\text{neither}} \neq \mu_{\text{slightly satisfied}}$
$\mu_{\text{neither}} \neq \mu_{\text{very satisfied}}$
$\mu_{\text{slightly satisfied}} \neq \mu_{\text{very satisfied}}$

Set significance level to $\alpha = 0.2$.

pairwise.t.test()

pairwise.t.test(stack_overflow$converted_comp, stack_overflow$job_sat, p.adjust.method = "none")

    Pairwise comparisons using t tests with pooled SD 

data:  stack_overflow$converted_comp and stack_overflow$job_sat 

                      Very dissatisfied Slightly dissatisfied Neither Slightly satisfied
Slightly dissatisfied 0.26860           -                     -       -                 
Neither               0.79578           0.36858               -       -                 
Slightly satisfied    0.29570           0.82931               0.41248 -                 
Very satisfied        0.34482           0.00384               0.15939 0.00084           

P value adjustment method: none

Significant differences: "Very satisfied" vs. "Slightly dissatisfied"; "Very satisfied" vs. "Neither"; "Very satisfied" vs. "Slightly satisfied"

As the no. of groups increases...

Scatter plot showing number of pairs vs. number of groups. As the number of groups increases, the number of pairs increases quadratically.

Scatter plot showing the probability of getting at least 1 significant result vs the number of groups. As the number of groups increases, the probability of having at least 1 significant result increases.

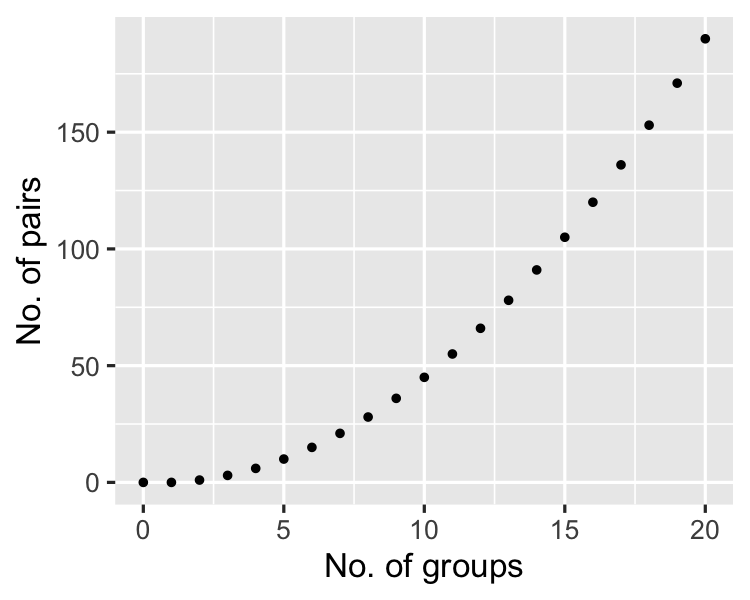
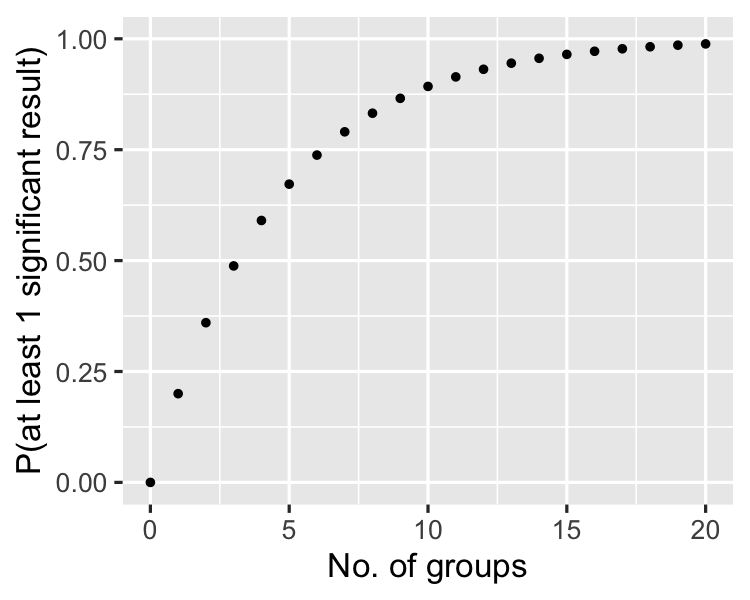
Bonferroni correction

pairwise.t.test(stack_overflow$converted_comp, stack_overflow$job_sat, p.adjust.method = "bonferroni")

    Pairwise comparisons using t tests with pooled SD 

data:  stack_overflow$converted_comp and stack_overflow$job_sat 

                      Very dissatisfied Slightly dissatisfied Neither Slightly satisfied
Slightly dissatisfied 1.0000            -                     -       -                 
Neither               1.0000            1.0000                -       -                 
Slightly satisfied    1.0000            1.0000                1.0000  -                 
Very satisfied        1.0000            0.0384                1.0000  0.0084            

P value adjustment method: bonferroni

Significant differences: "Very satisfied" vs. "Slightly dissatisfied"; "Very satisfied" vs. "Slightly satisfied"

More methods

p.adjust.methods

"holm"  "hochberg"  "hommel"  "bonferroni"  "BH"  "BY"  "fdr"  "none"

Bonferroni and Holm adjustments

p_values

0.268603 0.795778 0.295702 0.344819 0.368580 0.829315 0.003840 0.412482 0.159389 0.000838

Bonferroni

pmin(1, 10 * p_values)

1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 0.03840 1.00000 1.00000 0.00838

Holm (roughly)

pmin(1, 10:1 * sort(p_values))

0.00838 0.03456 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 0.82931

Let's practice!

Hypothesis Testing in R