Prior belief
Bayesian Data Analysis in Python

Michal Oleszak
Machine Learning Engineer
Prior distribution
- Prior distribution reflects what we know about the parameter before observing any data:
- nothing → uniform distribution (all values equally likely)
- old posterior → can be updated with new data
- One can choose any probability distribution as a prior to include external info in the model:
- expert opinion
- common knowledge
- previous research
- subjective belief
Prior's impact
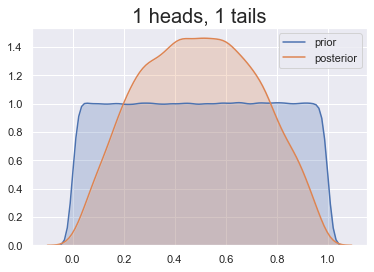
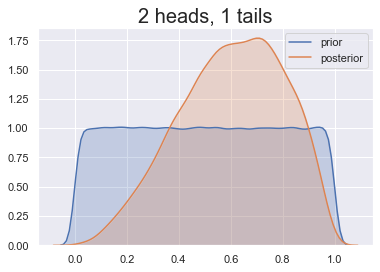
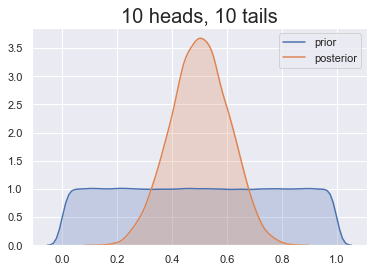
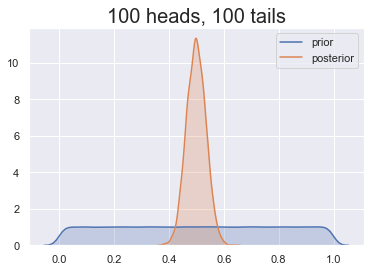
Prior distribution
- Prior distribution chosen before we see the data.
- Prior choice can impact posterior results (especially with little data).
- To avoid cherry-picking, prior choices should be:
- clearly stated,
- explainable: based on previous research, sensible assumptions, expert opinion, etc.
Choosing the right prior
Our prior belief: heads less likely
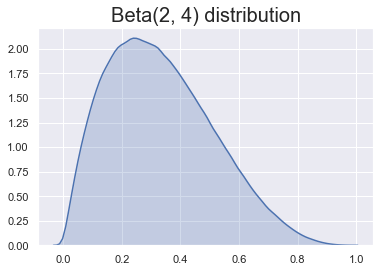
Some choices are better than others!
Conjugate priors
- Some priors, multiplied with specific likelihoods, yield known posteriors.
- They are known as conjugate priors.
- In the case of coin tossing:
- if we choose a prior Beta(a, b),
- then the posterior is Beta(#heads + a, #tosses - #heads + b)
- We can sample from the posterior using
numpy. get_heads_prob()from Chapter 1:def get_heads_prob(tosses): num_heads = np.sum(tosses) # prior: Beta(1,1) return np.random.beta(num_heads + 1, len(tosses) - num_heads + 1, 1000)
Two ways to get the posterior
Simulation
- If posterior is known, we can sample from it using
numpy:draws = np.random.beta(2, 4, 1000) - Outcome: an array of 1000 posterior draws:
array([0.05941031, ..., 0.70015975]) - Can be plotted with
sns.kdeplot(draws)
Calculation
- If posterior is not known, we can calculate it using grid approximation.
- Outcome: posterior probability for each grid element:
head_prob posterior_prob 0 0.00 0.009901 1 0.01 0.003624 ... ... 10199 0.99 0.003624 10200 1.00 0.009901 - Can be plotted with
sns.lineplot(df["head_prob"], df["posterior_prob"])
Let's practice working with priors!
Bayesian Data Analysis in Python

