A/B testing

Bayesian Data Analysis in Python

Michal Oleszak

Machine Learning Engineer

A/B testing

Randomized experiment: divide users in two groups (A and B)

Two groups of users.

¹ Picture: adapted from https://commons.wikimedia.org/wiki/File:A-B_testing_simple_example.png

A/B testing

Randomized experiment: divide users in two groups (A and B)
Expose each group to a different version of something (e.g. website layout)

Two groups of users being shown two different website layouts.

¹ Picture: adapted from https://commons.wikimedia.org/wiki/File:A-B_testing_simple_example.png

A/B testing

Randomized experiment: divide users in two groups (A and B)
Expose each group to a different version of something (e.g. website layout)
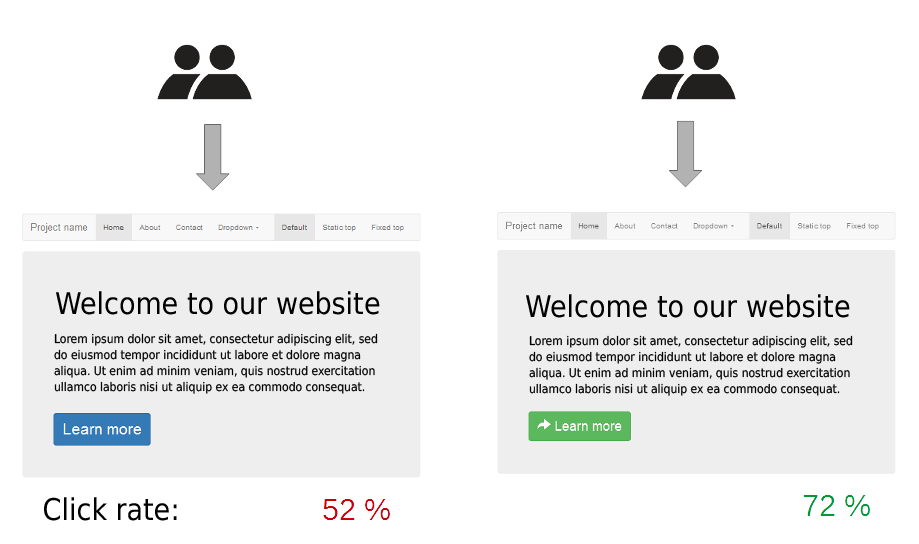
Compare which group scores better on some metric (e.g. click-through rate)

Two groups of users being shown two different website layouts, one of which has a higher click rate.

¹ Picture: adapted from https://commons.wikimedia.org/wiki/File:A-B_testing_simple_example.png

A/B testing: frequentist way

Based on hypothesis testing
Check whether A and B perform the same or not
Does not say how much better is A than B

A/B testing: Bayesian approach

Calculate posterior click-through rates for website layouts A and B and compare them
Directly calculate the probability that A is better than B
Quantify how much better it is
Estimate expected loss in case we make a wrong decision

A/B testing: Bayesian approach

When a user lands on the website, there are two scenarios:
- Click (success)
- No click (failure)
Use binomial distribution! (probability of success = click rate)

Simulate beta posterior

We know that if the prior is $Beta(a, b)$, then the posterior is $Beta(x, y)$, with:

$x = \text{NumberOfSuccesses} + a$

$y = \text{NumberOfObservations} - \text{NumberOfSuccesses} + b$

def simulate_beta_posterior(trials, beta_prior_a, beta_prior_b):
    num_successes = np.sum(trials)
    posterior_draws = np.random.beta(
      num_successes + beta_prior_a, 
      len(trials) - num_successes + beta_prior_b, 
      10000
    )
    return posterior_draws

Comparing posteriors

Lists of 1s (clicks) and 0s (no clicks):

print(A_clicks)
print(B_clicks)

[0 1 1 0 0 0 0 0 0 0 1 ... ]
[0 0 0 1 0 0 0 1 1 0 1 ... ]

Simulate posterior draws for each layout:

A_posterior = simulate_beta_posterior(A_clicks, 1, 1)
B_posterior = simulate_beta_posterior(B_clicks, 1, 1)

Plot posteriors:

sns.kdeplot(A_posterior, shade=True, label="A")
sns.kdeplot(B_posterior, shade=True, label="B")
plt.show()

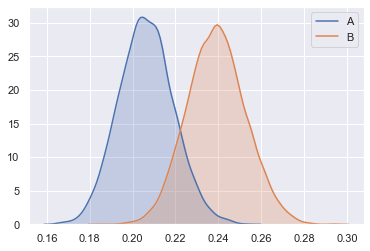
Two posteriors density plots, partially overlapping.

Comparing posteriors

Posterior difference between B and A:

diff = B_posterior - A_posterior

sns.kdeplot(diff, shade=True, label="difference: A-B")
plt.show()

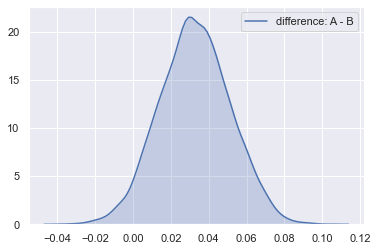
A density plot with almost all the probability mass above zero.

Probability of B being better:

(diff > 0).mean()

0.9639

Expected loss

If we deploy the worse website version, how many clicks do we lose?

# Difference (B-A) when A is better 
loss = diff[diff < 0]


# Expected (average) loss
expected_loss = loss.mean()
print(expected_loss)

-0.0077850237030215215

Ads data

print(ads)

                               user_id   product site_version                 time  banner_clicked
0     f500b9f27ac611426935de6f7a52b71f   clothes      desktop  2019-01-28 16:47:08               0
1     cb4347c030a063c63a555a354984562f  sneakers       mobile  2019-03-31 17:34:59               0
2     89cec38a654319548af585f4c1c76b51   clothes       mobile  2019-02-06 09:22:50               0
3     1d4ea406d45686bdbb49476576a1a985  sneakers       mobile  2019-05-23 08:07:07               0
4     d14b9468a1f9a405fa801a64920367fe   clothes       mobile  2019-01-28 08:16:37               0
...                                ...       ...          ...                  ...             ...
9995  7ca28ccde263a675d7ab7060e9ed0eca   clothes       mobile  2019-02-02 08:19:39               0
9996  7e2ec2631332c6c4527a1b78c7ede789   clothes       mobile  2019-04-04 03:27:05               0
9997  3b828da744e5785f1e67b5df3fda5571   clothes       mobile  2019-04-15 15:59:06               0
9998  6cce0527245bcc8519d698af2224c04a   clothes       mobile  2019-05-21 20:43:21               0
9999  8cf87a02f96327a1a8a93814f34d0d0c  sneakers       mobile  2019-03-02 21:27:57               0

Let's A/B test!

Bayesian Data Analysis in Python