Probability and Bayes' Theorem

Bayesian Data Analysis in Python

Michal Oleszak

Machine Learning Engineer

Probability theory

Statement of uncertainty.
A number between 0 and 1.
- P = 0 → impossible
- P = 1 → certain
- P = 0.5 → 50/50 chance

P(rain tomorrow) = 0.75 → 75% chance of rain tomorrow

Probability rules

Sum rule

Probability of A or B (independent events)
OR = addition
Probability of rolling 2 or 4 with a die

P(2 or 4) = 1/6 + 1/6 = 0.33333... = 33.3%

Product rule

Probability of A and B (independent events)
AND = multiplication
Probability of rolling 2 and then 4 with a die

P(2 and 4) = 1/6 * 1/6 = 0.02777... = 2.8%

Conditional probability

Probability of some event occurring, given that some other event has occurred.
P(A | B)

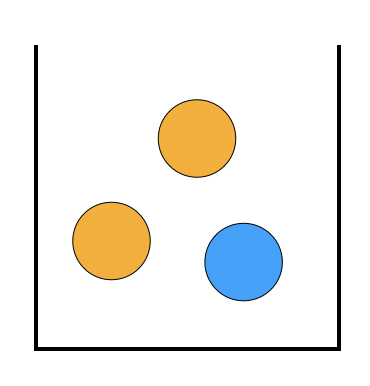
P(orange) = 2/3 → unconditional
P(blue) = 1/3 → unconditional

P(blue | orange) = 1/2 → conditional
P(orange | blue) = 1 → conditional

A schematic picture of three balls in a box. Two are orange, one is blue.

Bayes' Theorem

A way to calculate conditional probability when we know some other probabilities.

$$P(A|B) = \frac{P(B|A) * P(A)}{P(B)}$$

Bayes' Theorem

A way to calculate conditional probability when we know some other probabilities.

$$P(\text{accident}|\text{slippery}) = \frac{P(\text{slippery}|\text{accident}) * P(\text{accident})}{P(\text{slippery})}$$

road_conditions.head()

     accident   slippery
0       False       True
1        True       True
2       False      False
3       False      False
4       False      False

Bayes' Theorem in practice

$$P(\text{accident}|\text{slippery}) = \frac{P(\text{slippery}|\text{accident}) * P(\text{accident})}{P(\text{slippery})}$$

# Unconditional probability of an accident
p_accident = road_conditions["accident"].mean()  # 0.0625


# Unconditional probability of the road being slippery
p_slippery = road_conditions["slippery"].mean()  # 0.0892


# Probability of the road being slippery given there is an accident
p_slippery_given_accident = road_conditions.loc[road_conditions["accident"]]["slippery"].mean()  # 0.7142


# Probability of an accident given the road is slippery
p_accident_given_slippery = p_slippery_given_accident * p_accident / p_slippery  # 0.5

Let's practice!

Bayesian Data Analysis in Python