Regression and forecasting

Bayesian Data Analysis in Python

Michal Oleszak

Machine Learning Engineer

Linear regression

$$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ...$$

$$\text{sales} = \beta_0 + \beta_1\text{marketingSpending}$$

Frequentist inference:
- $\text{sales} = \beta_0 + \beta_1\text{marketingSpending} + \varepsilon$
- $\varepsilon \sim \mathcal{N} (0, \sigma)$

Bayesian inference:
- $\text{sales} \sim \mathcal{N} (\beta_0 + \beta_1\text{marketingSpending}, \sigma)$

Normal distribution

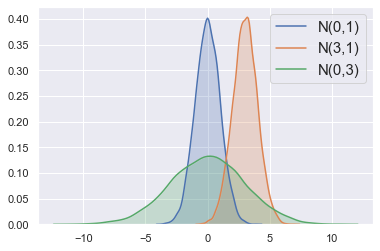
normal_0_1 = np.random.normal(0, 1, size=10000)




sns.kdeplot(normal_0_1, shade=True, label="N(0,1)")



plt.show()

A density of the standard normal distribution, peaking at 0 and symmetric around it.

Normal distribution

normal_0_1 = np.random.normal(0, 1, size=10000)
normal_3_1 = np.random.normal(3, 1, size=10000)


sns.kdeplot(normal_0_1, shade=True, label="N(0,1)")
sns.kdeplot(normal_3_1, shade=True, label="N(3,1)")


plt.show()

A density of the standard normal distribution, peaking at 3 and symmetric around it.

Normal distribution

normal_0_1 = np.random.normal(0, 1, size=10000)
normal_3_1 = np.random.normal(3, 1, size=10000)
normal_0_3 = np.random.normal(0, 3, size=10000)

sns.kdeplot(normal_0_1, shade=True, label="N(0,1)")
sns.kdeplot(normal_3_1, shade=True, label="N(3,1)")
sns.kdeplot(normal_0_3, shade=True, label="N(0,3)")

plt.show()

A density of the standard normal distribution, peaking at 0 and symmetric around it.

Bayesian regression model definition

$$\text{sales} \sim \mathcal{N} (\beta_0 + \beta_1\text{marketingSpending}, \sigma)$$

$$\beta_0 \sim \mathcal{N} (5, 2)$$

$$\beta_1 \sim \mathcal{N} (2, 10)$$

$$\sigma \sim \mathcal{Unif} (0, 3)$$

We expect $5000 sales without any marketing.
We expect $2000 increase in sales from each 1000 increase in spending.
Uniform prior for standard deviation, as we don't know what it could be.

Estimating regression parameters

Grid approximation → impractical for many parameters
Choose conjugate priors and simulate from a known posterior → unintuitive priors
Third way: simulate from the posterior even with non-conjugate priors!
For now, assume the parameter draws are given

Plot posterior

$$\text{sales} = \beta_0 + \beta_1\text{marketingSpending}$$

print(marketing_spending_draws)

array([9.6153, 8.9922, ..., 4.59565])

import pymc3 as pm

pm.plot_posterior(
  marketing_spending_draws, 
  hdi_prob=0.95
)

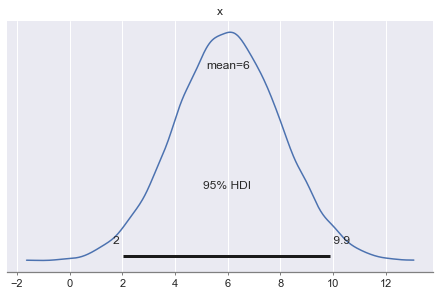
A density plot with the mean and the credible interval marked on it.

Posterior draws analysis

posterior_draws_df = pd.DataFrame({
    "intercept_draws": intercept_draws,
    "marketing_spending_draws": marketing_spending_draws,
    "sd_draws": sd_draws
})

print(posterior_draws_df)

       intercept_draws  marketing_spending_draws      sd_draws
count     10000.000000              10000.000000  10000.000000
mean          2.972130                  5.999146      1.337621
std           3.008565                  2.020708      0.471723
min          -8.562093                 -2.842438      0.029643
25%           0.972832                  4.621807      1.003229
50%           3.002940                  5.975067      1.427617
75%           5.020615                  7.362572      1.736310
max          15.228549                 13.258955      1.999834

Predictive distribution

How much sales can we expect if we spend $1000 on marketing?

$\text{sales} \sim \mathcal{N} (\beta_0 + \beta_1\text{marketingSpending}, \sigma)$

# Get point estimates of parameters
intercept_mean = intercept_draws.mean()
marketing_spending_mean = marketing_spending_draws.mean()
sd_mean = sd_draws.mean()


# Calculate mean of predictive distribution
predictive_mean = intercept_mean + marketing_spending_mean * 1000


# Simulate from predictive distribution
prediction_draws = np.random.normal(predictive_mean, sd_mean, size=10000)

Predictive distribution

How much sales can we expect if we spend $1000 on marketing?

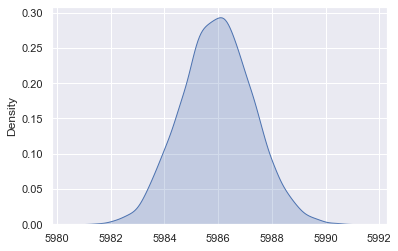
A bell-shaped density of predicted sales peaking around 5986.

Let's regress and forecast!

Bayesian Data Analysis in Python