Fitting the Weibull model
Survival Analysis in Python

Shae Wang
Senior Data Scientist
Probability distributions
A probability distribution
A mathematical function that describes the probability of different event outcomes.
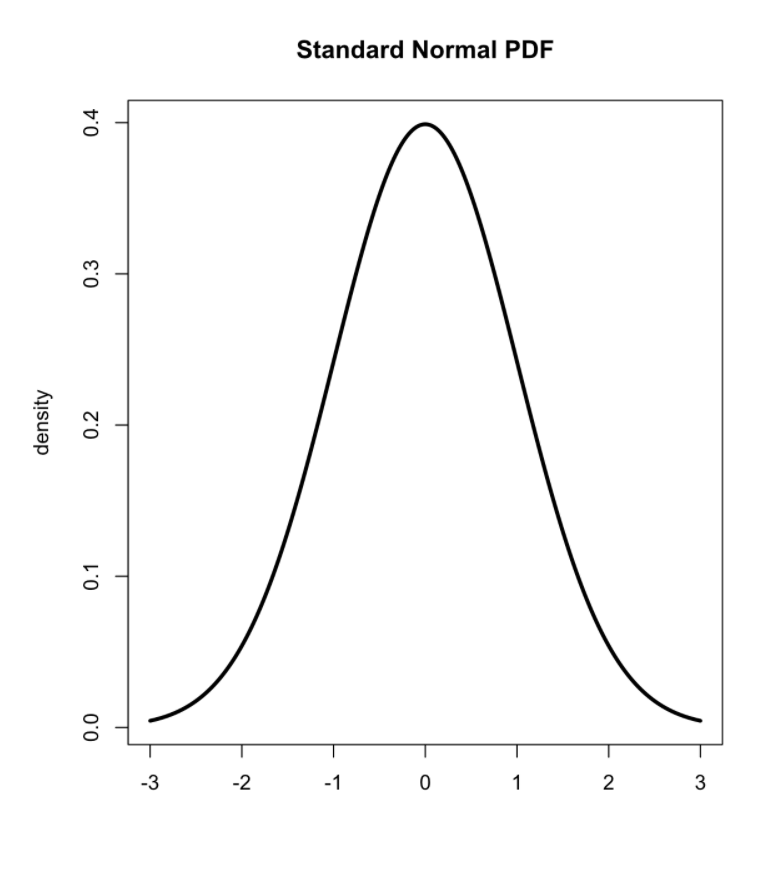
Probability distributions
A probability distribution
A mathematical function that describes the probability of different event outcomes.
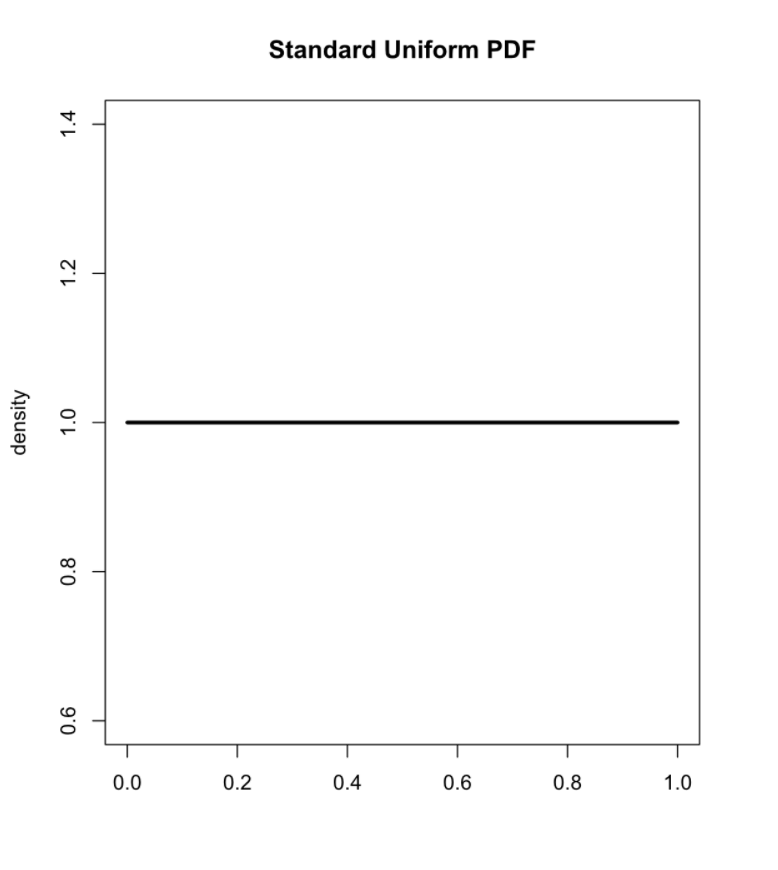
Introducing the Weibull distribution
The Weibull distribution
A continuous probability distribution that models time-to-event data very well (but originally applied to model particle size distribution).
The Weibull probability density function
$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k}$$ $$x\geq0,k>0,\lambda>0$$
Introducing the Weibull distribution
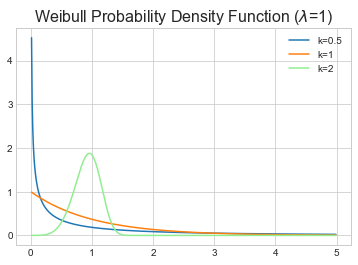
$k$
Determines the shape
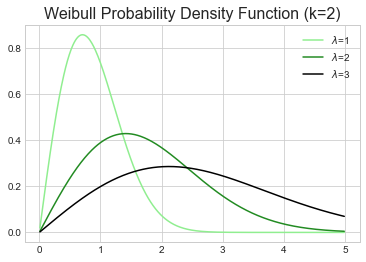
$\lambda$
Determines the scale
Fitting the Weibull distribution to data
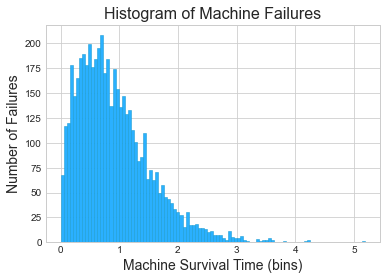
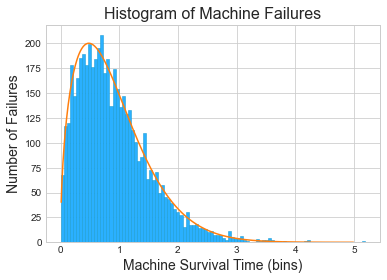
A company maintains a fleet of machines that are prone to failure...
Fitting the Weibull distribution to data
A company maintains a fleet of machines that are prone to failure...
From Weibull distribution to survival function
$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k} \quad\rightarrow\quad\qquad\qquad S(t)=e^{-(t/\lambda)^\rho}$$
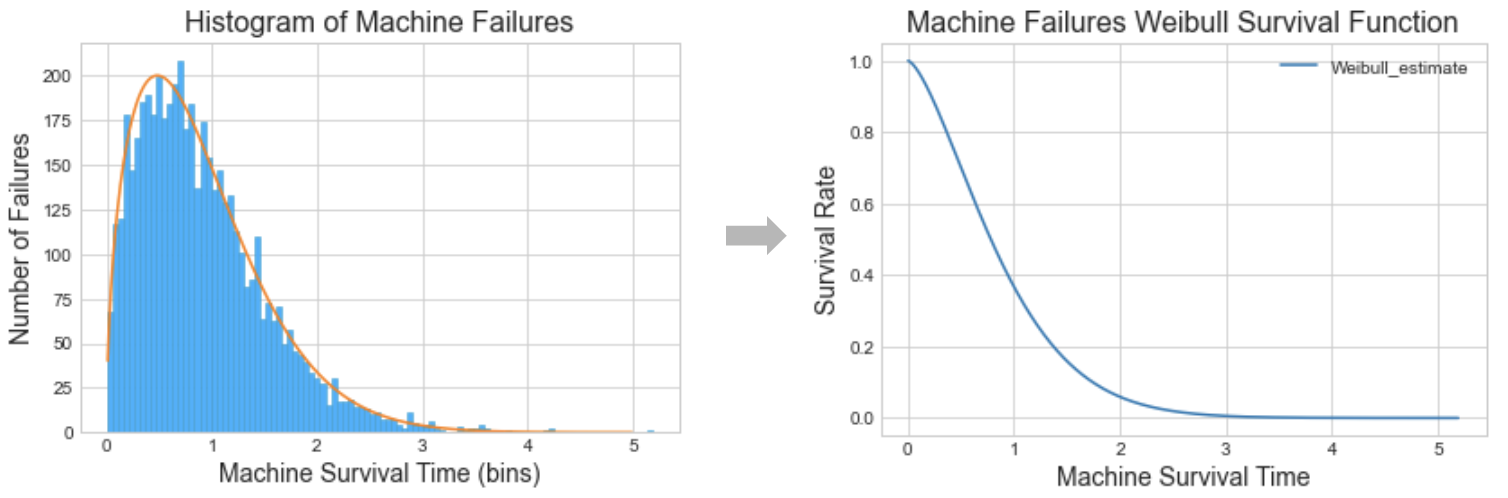
$\rho$ is same as k
The knobs: k and lambda
k and $\lambda$
- k (or $\rho$): determines the shape
- $\lambda$: determines the scale (indicates when 63.2% of the population has experienced the event)
$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k} \quad\rightarrow\quad f(x;\lambda,k=3)=\frac{3}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^2e^{-(x/\lambda)^3}$$
- Weibull distribution: the failure/event rate is proportional to a power of time.
Interpreting k (or $\rho$)
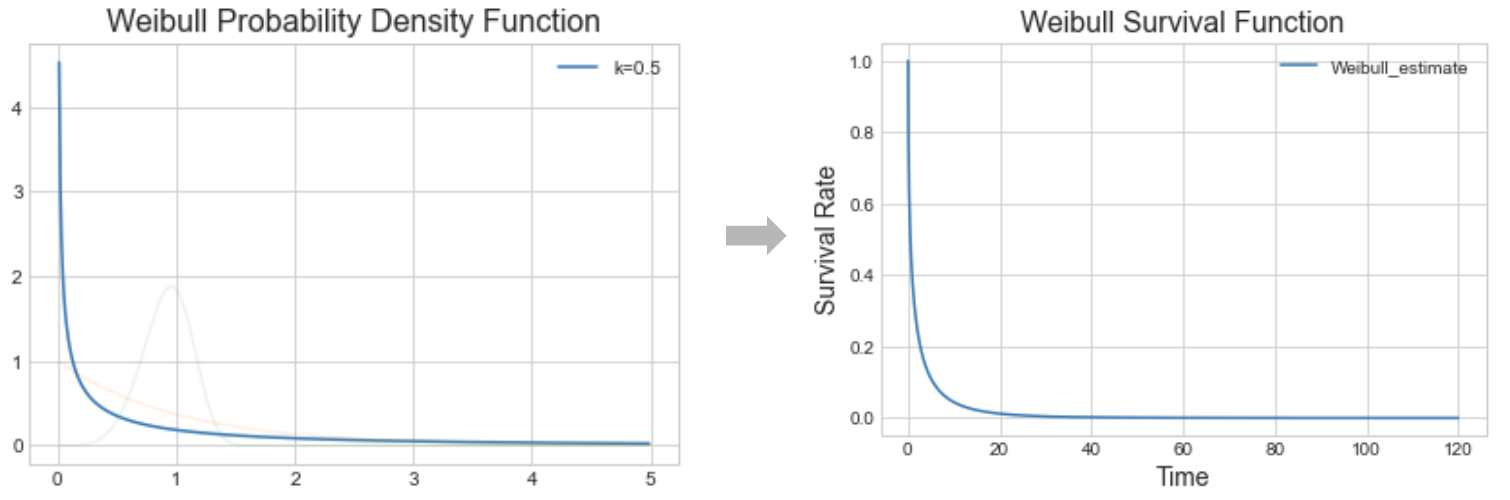
- When $k<1$, the failure/event rate decreases over time.
Interpreting k (or $\rho$)
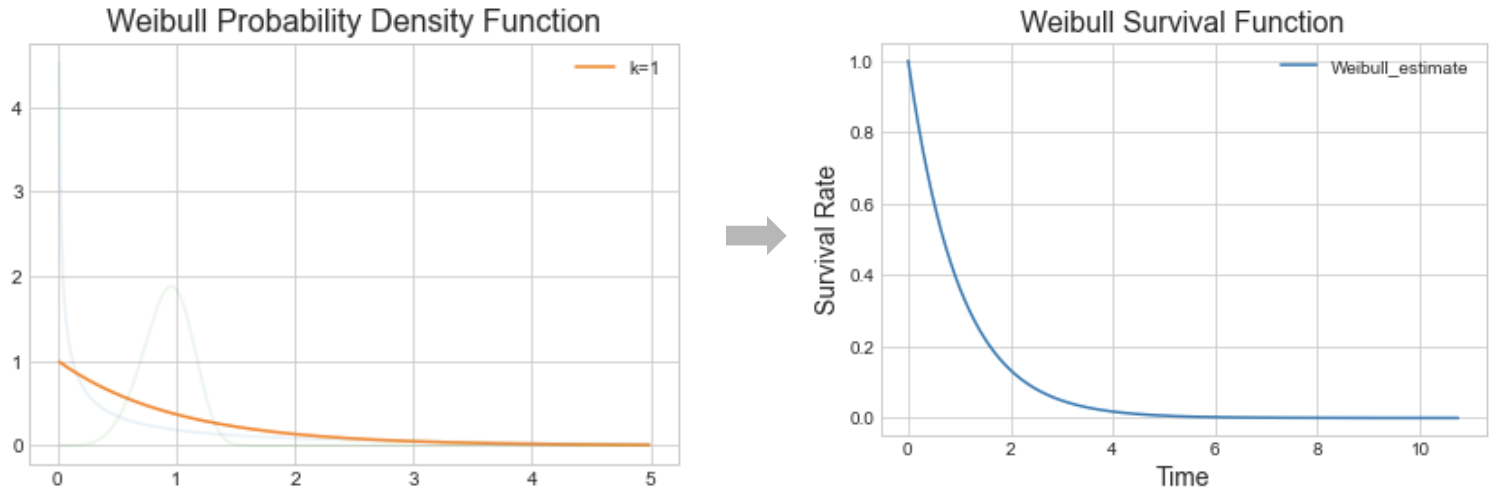
- When $k=1$, the failure/event rate is constant over time.
Interpreting k (or $\rho$)
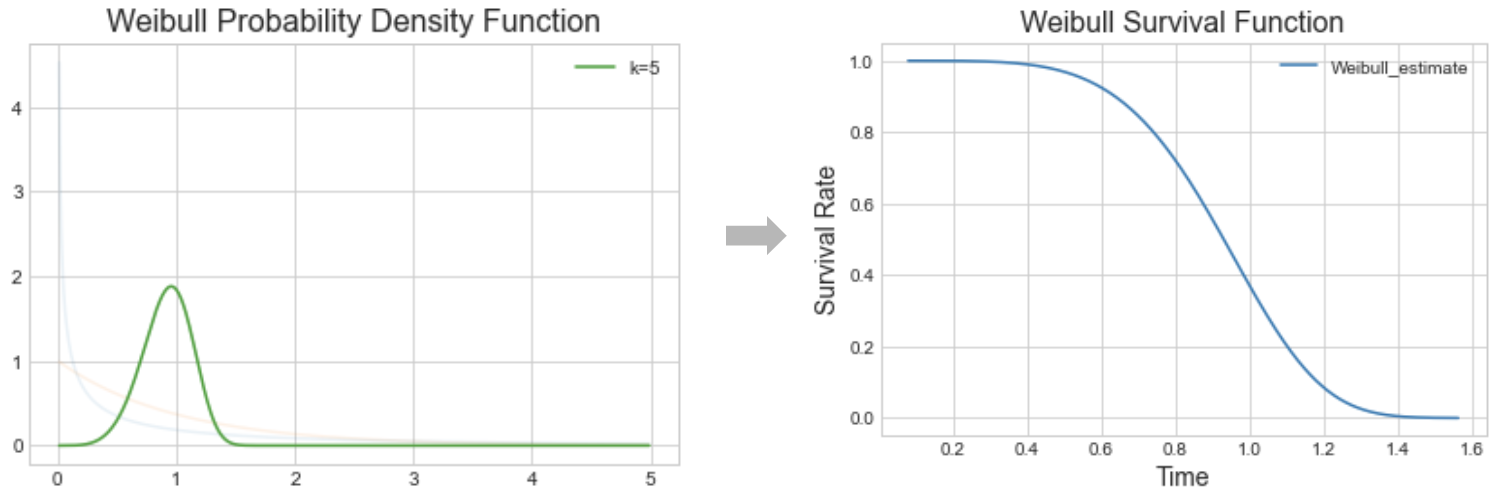
- When $k>1$, the failure/event rate increases over time.
Survival analysis with Weibull distribution
- Import the
WeibullFitterclassfrom lifelines import WeibullFitter - Instantiate a
WeibullFitterclasswb = WeibullFitter() - Call
.fit()to fit the estimator to the datawb.fit(durations, event_observed) - Access
.survival_function_,.lambda_,.rho_,.summary,.predict()
Example Weibull model
DataFrame name: mortgage_df
| id | duration | paid_off |
|---|---|---|
| 1 | 25 | 0 |
| 2 | 17 | 1 |
| 3 | 5 | 0 |
| ... | ... | ... |
| 1000 | 30 | 1 |
from lifelines import WeibullFitter
wb = WeibullFitter()
wb.fit(durations=mortgage_df["duration"],
event_observed=mortgage_df["paid_off"])
Example Weibull model
wb.survival_function_.plot()
plt.show()
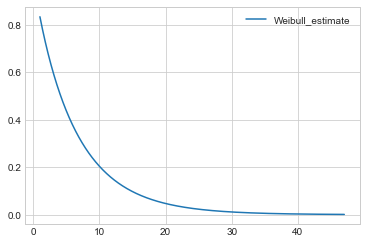
print(wb.lambda_, wb.rho_)
6.11 0.94
print(wb.predict(20))
0.05
Let's practice!
Survival Analysis in Python

