Weibull model with covariates

Survival Analysis in Python

Shae Wang

Senior Data Scientist

Comparing survival functions

Compare groups using the Kaplan-Meier estimator:

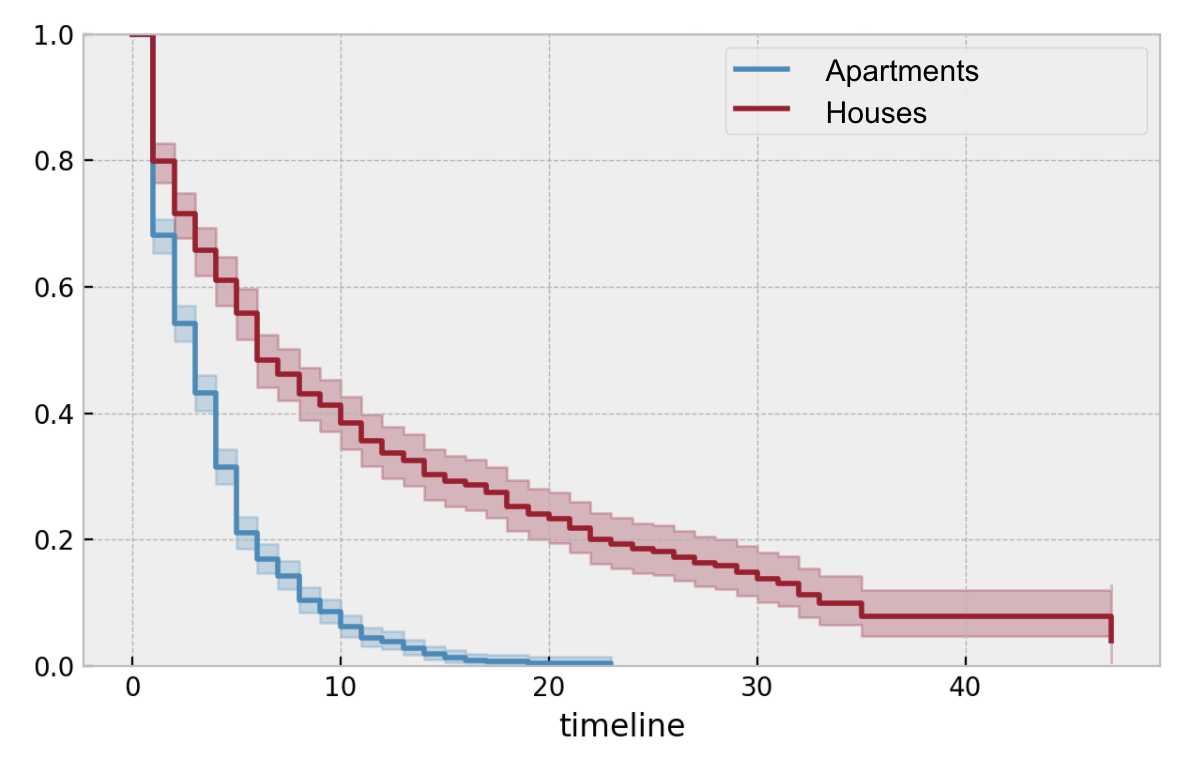
Apartment vs. house Kaplan-Meier survival curves.

Compare groups using the log-rank test:

<lifelines.StatisticalResult: logrank_test>
 null_distribution = chi squared
degrees_of_freedom = 1
         test_name = logrank_test
 test_statistic    p  -log2(p)
           0.09 0.77      0.38

Q: How do we assess if/how one or multiple continuous variables affect the survival function?

Survival regression

A method that models survival functions with covariates
Quantifies how each covariate affects the survival function

$$Y_i=f(X_i,\beta)$$

$$Y_i: \text{durations}, X_i: \text{covariates}$$

Example covariates: age, weight, country

The Accelerated Failure Time (AFT) model

$$\text{Population A}: S_A(t)$$

$$\text{Population B}: S_B(t)$$

$$S_A(t)=S_B(t*\lambda)$$

$S_B(t)$ is speeding up (accelerating) or slowing down (decelerating) along $S_A(t)$ by a factor of $\lambda$.
AFT models this acceleration/deceleration relationship based on model covariates.
When a covariate changes from $a$ to $b$, time-to-event speeds up or slows down by the accelerated failure rate $\lambda$.
Example: $S_{dog}(t)=S_{human}(t*7)$

Data for survival regression

DataFrame example: mortgage_df

id	property_type	principal	interest	property_tax	credit_score	duration	paid_off
1	house	1275	0.035	0.019	780	25	0
2	apartment	756	0.028	0.020	695	17	1
3	apartment	968	0.029	0.017	810	5	0
...	...	...	...	...	...	...	...
1000	house	1505	0.041	0.023	750	30	1

Combining Weibull with AFT: the Weibull AFT model

DataFrame: mortgage_df
Covariates:
- property_type is replaced with a dummy variable:
  - house: 1 if "house", 0 if "apartment"
- principal
- interest
- property_tax
- credit_score

Import and instantiate the WeibullAFTFitter class

from lifelines import WeibullAFTFitter
aft = WeibullAFTFitter()

Call .fit() to fit the estimator to the data

aft.fit(df=mortgage_df,
     duration_col="duration",
     event_col="paid_off")

Interpreting model output

print(aft.summary)

<lifelines.WeibullAFTFitter: fitted with 1808 observations, 340 censored>
                      coef  exp(coef)  se(coef)      z       p
lambda_ house         0.04       1.04      0.01   0.99    0.32  
        principal    -0.03       0.97      0.22  -1.04    0.30  
        interest      0.11       1.11      0.15   1.96    0.05  
        property_tax  0.31       1.36      0.27   1.15    0.25  
        credit_score -0.16       0.85      0.14  -2.33    0.02  
        Intercept     3.99      54.06      0.41   9.52 <0.0005   
rho_    Intercept     0.34       1.40      0.08   3.80 <0.0005

WeibullAFTFitter with custom formula

Using formula to handle custom model covariates:

aft.fit(df=mortgage_df,
        duration_col="duration",
        event_col="paid_off",
        formula="principal + interest * house")

Analogous to the linear model with interaction term:

$\beta_1$principal$+\beta_2$interest$+\beta_3$house$+\beta_4$interest$\cdot$house

Interpreting model output

print(aft.summary)

<lifelines.WeibullAFTFitter: fitted with 1808 observations, 340 censored>
                       coef  exp(coef)  se(coef)      z       p
lambda_ principal     -0.03       0.97      0.22  -1.04    0.30     
        interest       0.11       1.11      0.15   1.96    0.05  
        house          0.04       1.04      0.01   0.99    0.32  
        interest:house 0.06       1.06      0.14   0.42    0.64
        Intercept      3.99      54.06      0.41   9.52 <0.0005   
rho_    Intercept      0.34       1.40      0.08   3.80 <0.0005

Let's practice!

Survival Analysis in Python