Factors affecting convexity

Bond Valuation and Analysis in Python

Joshua Mayhew

Options Trader

Convexity is a benefit

Bond prices rise more when yields decrease, fall less when yields increase

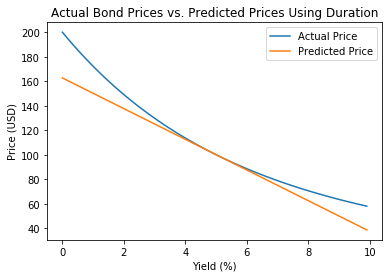
Investigating convexity

Compare the convexity of two bonds directly
Plot a graph of factor against convexity
Directly examine the curvature of the price/yield relationship

Coupon vs. convexity

10 year bonds with 5% yield, first pays no coupon, second pays 10% coupon

price_1 = -npf.pv(rate=0.05, nper=10, pmt=0, fv=100)

price_up_1 = -npf.pv(rate=0.06, nper=10, pmt=0, fv=100)

price_down_1 = -npf.pv(rate=0.04, nper=10, pmt=0, fv=100)

convexity_1 = (price_down_1 + price_up_1 - 2 * price_1) / (price_1 * 0.01 ** 2)

price_2 = -npf.pv(rate=0.05, nper=10, pmt=10, fv=100)
price_up_2 = -npf.pv(rate=0.06, nper=10, pmt=10, fv=100)
price_down_2 = -npf.pv(rate=0.04, nper=10, pmt=10, fv=100)
convexity_2 = (price_down_2 + price_up_2 - 2 * price_2) / (price_2 * 0.01 ** 2)

print("Low Coupon Bond Convexity: ", convexity_1)
print("High Coupon Bond Convexity: ", convexity_2)

Low Coupon Bond Convexity:  99.89
High Coupon Bond Convexity:  64.09

Maturity vs. convexity

bond_yields = np.arange(0, 20, 0.1)
bond = pd.DataFrame(bond_yields, columns=['yield'])

bond['price_10y'] = -npf.pv(rate=bond['yield'] / 100, 
    nper=10, pmt=0, fv=100)
bond['price_30y'] = -npf.pv(rate=bond['yield'] / 100, 
    nper=30, pmt=0, fv=100)

plt.plot(bond['yield'], bond['price_10y'])
plt.plot(bond['yield'], bond['price_30y'])
plt.xlabel('Yield (%)')
plt.ylabel('Price (USD)')
plt.title('Bond Maturity vs. Convexity')
plt.legend(["10 Year Bond", "30 Year Bond"])
plt.show()

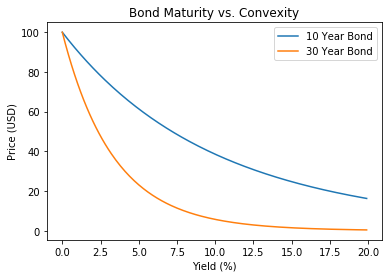
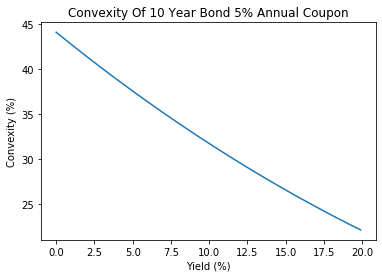
Yield vs. convexity

bond_yields = np.arange(0, 20, 0.1)
bond = pd.DataFrame(bond_yields, columns=['bond_yield'])

bond['price'] = -npf.pv(rate=bond['bond_yield'] / 100, 
    nper=10, pmt=5, fv=100)

bond['price_up'] = -npf.pv(rate=bond['bond_yield'] / 100 
    + 0.01, nper=10, pmt=5, fv=100)

bond['price_down'] = -npf.pv(rate=bond['bond_yield'] / 100 
    - 0.01, nper=10, pmt=5, fv=100)

bond['convexity'] = (bond['price_down'] + bond['price_up'] 
- 2 * bond['price']) / (bond['price'] * 0.01 ** 2)

plt.plot(bond['bond_yield'], bond['convexity'])
plt.xlabel('Yield (%)')
plt.ylabel('Convexity (%)')
plt.title("Convexity Of 10 Year Bond 5% Annual Coupon")
plt.show()

Summary

Positive convexity is a benefit:
- Lose less when yields rise, make more when yields fall

Convexity increases when a bond has a:
- Higher maturity
- Lower coupon
- Lower yield

Let's practice!

Bond Valuation and Analysis in Python