Present value & zero coupon bonds

Bond Valuation and Analysis in Python

Joshua Mayhew

Options Trader

Present Value

Money compounds from its value today to its value in the future
This process also works in reverse

Present Value

We can rearrange our compound interest equation from earlier:

$FV = PV \times (1 + r)^n$

$PV = \frac{FV}{(1 + r)^n}$

Called "discounting to present value" or just "discounting"

Present Value

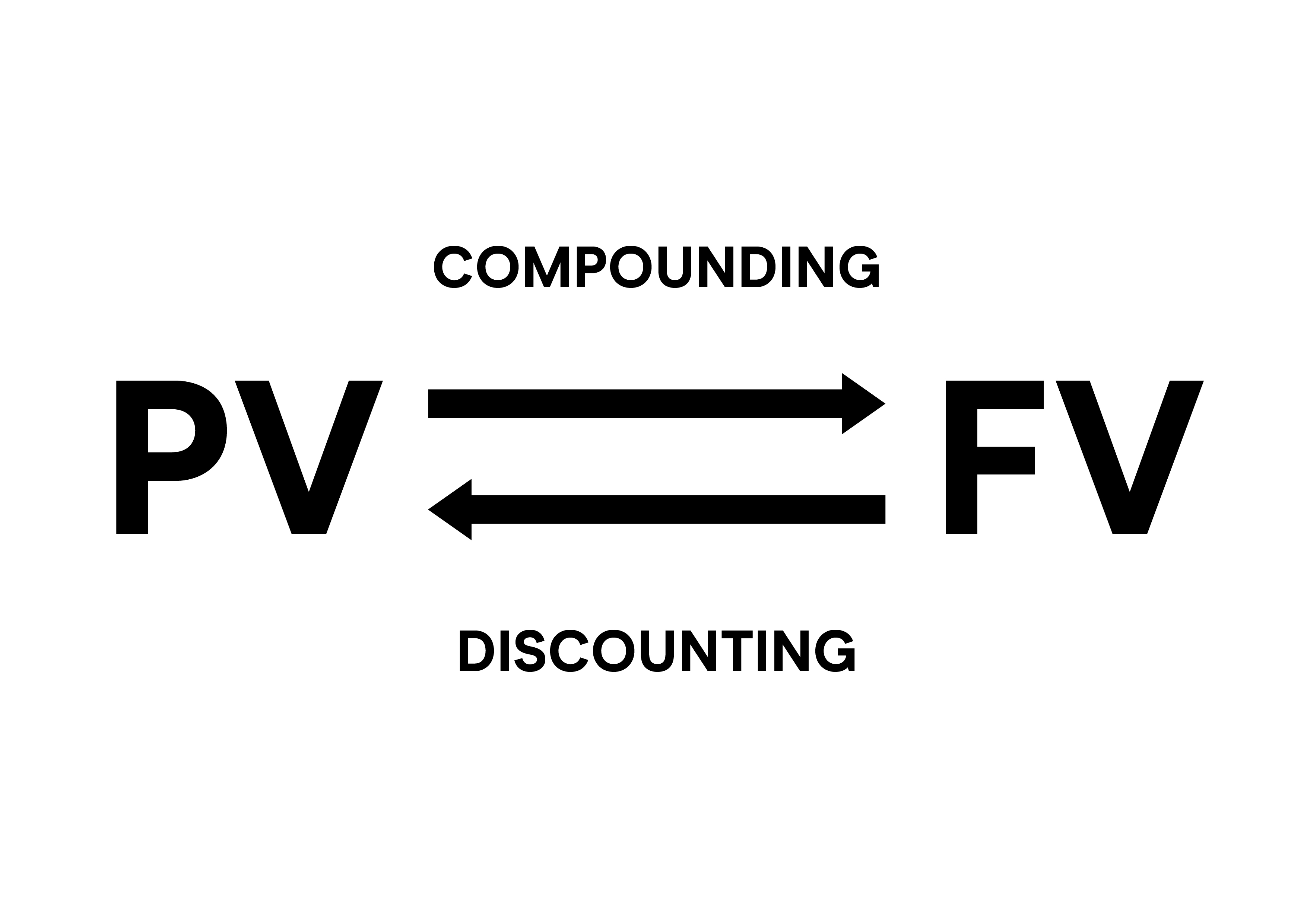
To move from present value to future value, we compound
To move from future value to present value, we discount

Present Value

A higher interest rate or longer time period increases the FV
So a higher interest rate or longer time period must decrease the PV

The pv() function

import numpy_financial as npf
?npf.pv

Signature: npf.pv(rate, nper, pmt, fv=0)
Docstring: Compute the present value.


Given:
 * a future value, `fv`

 * an interest `rate` compounded once per period, of which there are

 * `nper` total

 * a (fixed) payment, `pmt`


Return: the value now

The pv() function

How much should we invest now at 5% per year to have USD 10,000 in 10 years?

import numpy_financial as npf
npf.pv(rate=0.05, nper=10, pmt=0, fv=10000)

-6139.13

-npf.pv(rate=0.05, nper=10, pmt=0, fv=10000)

6139.13

The pv() function

Or, by rearranging our compound interest equation from earlier:

pv = 10000 / (1 + 0.05) ** 10
print(pv)

6139.13

Bonds introduction

Debt instrument, issued by governments and companies
Investors buy bonds in exchange for interest
Provide relatively safe and consistent returns
Are usually less risky and volatile than stocks

Zero coupon bonds

Pays a single cash-flow called the face value
Paid at a single point in time called the maturity
No intermediate cash-flows (called coupons) paid until maturity, hence the name
Their price is the PV of the single cash-flow

Zero coupon bonds

Usually issued at a discount to their face value
This difference is called the yield (measured in percent)

Zero coupon bonds

Let's look at an example of a zero coupon bond that:

Has a 3 year maturity
A face value of USD 100
A yield of 3.5%

What is the price of this bond?

Zero coupon bonds

Zero coupon bond with a 3 year maturity that yields 3.5% and has a face value of USD 100:

import numpy_financial as npf
-npf.pv(rate=0.035, nper=3, pmt=0, fv=100)

90.19

Or, again by rearranging our compound interest equation from earlier:

pv = 100 / (1 + 0.035) ** 3
print(pv)

90.19

Let's practice!

Bond Valuation and Analysis in Python