Convexity

Bond Valuation and Analysis in Python

Joshua Mayhew

Options Trader

Plotting predicted vs. actual prices

import numpy as np
import numpy_financial as npf
import pandas as pd
import matplotlib.pyplot as plt

price = -npf.pv(rate=0.05, nper=20, pmt=5, fv=100)
price_up = -npf.pv(rate=0.06, nper=20, pmt=5, fv=100)
price_down = -npf.pv(rate=0.04, nper=20, pmt=5, fv=100)
duration = (price_down - price_up) / (2 * price * 0.01)
dollar_duration = duration * price * 0.01
print("Bond Price (USD): ", price)
print("Dollar Duration (USD): ", dollar_duration)

Bond Price (USD): 100.00
Dollar Duration (USD): 12.53

Plotting predicted vs. actual prices

bond_yields = np.arange(0, 10, 0.1)
bond = pd.DataFrame(bond_yields, columns=['bond_yield'])
bond['price'] = -npf.pv(rate=bond['bond_yield'] / 100, nper=20, pmt=5, fv=100)

    bond_yield       price
0          0.0  200.000000
1          0.1  196.978503
..         ...         ...
98         9.8   58.570780
99         9.9   57.997210

[100 rows x 2 columns]

Plotting predicted vs. actual prices

bond['yield_change'] = bond['bond_yield'] - 5

    bond_yield       price  yield_change
0          0.0  200.000000        -5.0
1          0.1  196.978503        -4.9
2          0.2  194.013231        -4.8
..         ...         ...           ...
97         9.7   59.153044         4.7
98         9.8   58.570780         4.8
99         9.9   57.997210         4.9

[100 rows x 3 columns]

Plotting predicted vs. actual prices

$ \text{Price Change} = -100 \times \text{Dollar Duration} \times \Delta y$

bond['price_change'] = -100 * dollar_duration * bond['yield_change'] / 100

    bond_yield       price  yield_change  price_change
0          0.0  200.000000          -5.0     62.650619
1          0.1  196.978503          -4.9     61.397607
..         ...         ...           ...           ...
98         9.8   58.570780           4.8    -60.144594
99         9.9   57.997210           4.9    -61.397607

[100 rows x 4 columns]

Plotting predicted vs. actual prices

bond['predicted_price'] = price + bond['price_change']

   bond_yield       price  yield_change  price_change  predicted_price
0          0.0  200.000000          -5.0     62.650619       162.650619
1          0.1  196.978503          -4.9     61.397607       161.397607
2          0.2  194.013231          -4.8     60.144594       160.144594
..         ...         ...           ...           ...              ...
97         9.7   59.153044           4.7    -58.891582        41.108418
98         9.8   58.570780           4.8    -60.144594        39.855406
99         9.9   57.997210           4.9    -61.397607        38.602393

[100 rows x 5 columns]

Plotting predicted vs. actual prices

plt.plot(bond['bond_yield'], bond['price'])
plt.plot(bond['bond_yield'], bond['predicted_price'])
plt.xlabel('Yield (%)')
plt.ylabel('Price (USD)')
plt.title("Actual Bond Prices vs. 
    Predicted Prices Using Duration")
plt.legend(["Actual Price", "Predicted Price"])
plt.show()

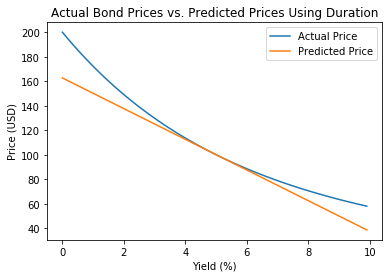
Limitations of duration

Duration is a linear measure
Bond prices are convex
Duration is accurate for small yield changes only

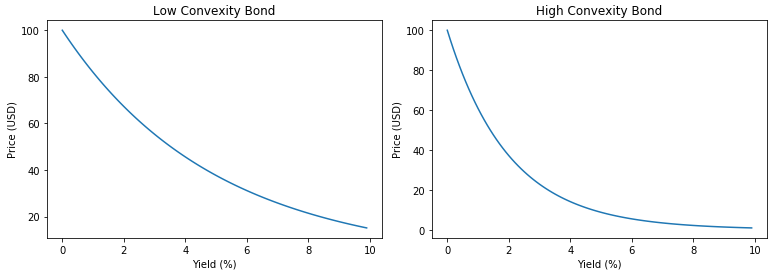
What is convexity?

Measures the curvature of bond prices
Used to improve bond price prediction and risk measurement
Higher convexity = more curved price/yield relationship

Convexity formula

We will use a simplified formula for convexity:

${\large Convexity = \frac{P_{down}\ +\ P_{up} \ - \ 2\times P}{P\ \times\ (\Delta y)^2}}$

$P_{down}$ = Bond price at 1% lower yield
$P_{up}$ = Bond price at 1% higher yield
$2 \times P$ = Double the bond price at current yield
$(\Delta y)^2$ = Change in yield squared (we will use 1% ^ 2)

Convexity example

10 year bond, 5% annual coupon, 4% yield to maturity, what is its convexity?

${ Convexity = \frac{P_{down}\ +\ P_{up} \ - \ 2\times P}{P\ \times\ (\Delta y)^2}}$

price = -npf.pv(rate=0.04, nper=10, pmt=5, fv=100)

price_up = -npf.pv(rate=0.05, nper=10, pmt=5, fv=100)
price_down = -npf.pv(rate=0.03, nper=10, pmt=5, fv=100)

convexity = (price_down + price_up - 2 * price) / (price * 0.01 ** 2)
print("Convexity: ", convexity)

Convexity:  77.56

Summary

Duration is a linear measure
Bond prices are curved
Duration is accurate for small yield changes only
Convexity measures this curvature

${ Convexity = \frac{P_{down}\ +\ P_{up} \ - \ 2\times P}{P\ \times\ (\Delta y)^2}}$

Let's practice!

Bond Valuation and Analysis in Python