Coupon paying bonds

Bond Valuation and Analysis in Python

Joshua Mayhew

Options Trader

Coupon bond definition

Pays regular cash-flows (coupons) during its life
At maturity it pays both a coupon and the face value
Coupons are typically paid annually or semi-annually
The number of coupons paid per year is called the frequency
Its yield to maturity is the annual return from buying and holding the bond to maturity

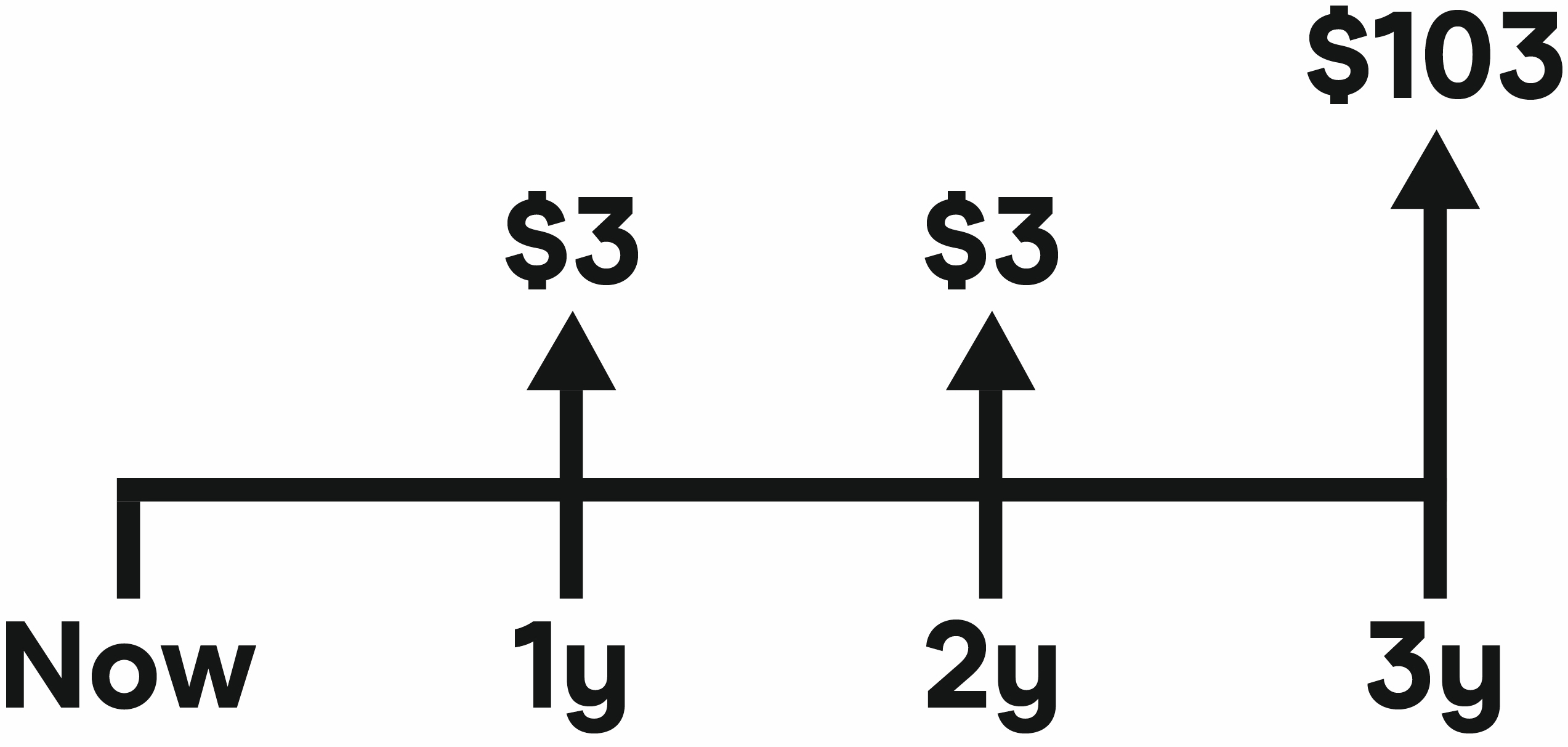
Take a 3 year bond with a 3% annual coupon, face value of USD 100, and yield of 4%:

WARNING: The coupon is fixed and doesn't change!

We break the bond up into a collection of zero coupon bonds, then price these:

3 year bond with a 3% annual coupon, face value of USD 100, and yield of 4%

Using our compound interest formula from earlier:

$ \text{1yr ZCB Price: } \frac{3}{(1 + 0.04)^1} = 2.88$

$ \text{2yr ZCB Price: } \ \frac{3}{(1 + 0.04)^2} = 2.77$

$ \text{3yr ZCB Price: } \ \frac{103}{(1 + 0.04)^3} = 91.57$

$\text{Coupon Bond Price: } 2.88 + 2.77 + 91.57 = 97.22$

More generally, our formula for the price of a coupon bond is:

$ Price = PV = \frac{C}{(1 + r)^1} + \frac{C}{(1 + r)^2} + ... +\frac{C}{(1 + r)^n} + \frac{P}{(1 + r)^n}$

$ = (\sum_{i=1}^n \frac{C}{(1 + r)^i}) + \frac{P}{(1 + r)^n}$

Taking the same 3 year bond with an annual coupon of 3% and yield to maturity of 4%:

import numpy_financial as npf
-npf.pv(rate=0.04, nper=3, pmt=3, fv=100)

97.22

We set pmt to be positive.

We also put a minus sign before the function.

We set fv to 100 not 103.

Bond Valuation and Analysis in Python