Predictions and odds ratios

Introduction to Regression with statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

The regplot() predictions

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

plt.show()

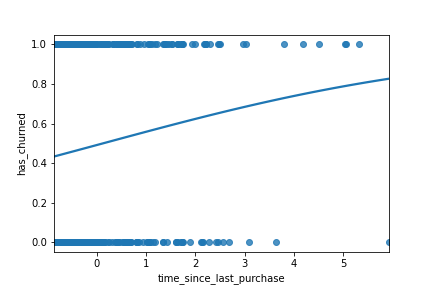
A scatter plot of churn versus time since last purchase, with a logistic trend line.

Making predictions

mdl_recency = logit("has_churned ~ time_since_last_purchase",
                    data = churn).fit()


explanatory_data = pd.DataFrame(
  {"time_since_last_purchase": np.arange(-1, 6.25, 0.25)})


prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))

Adding point predictions

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="has_churned",
                data=prediction_data,
                color="red")

plt.show()

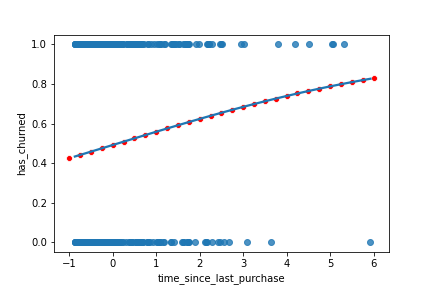
The scatter plot of churn versus time since last purchase, with a logistic trend line. The plot is annotated with the results from predict(), which follow the trend line exactly.

Getting the most likely outcome

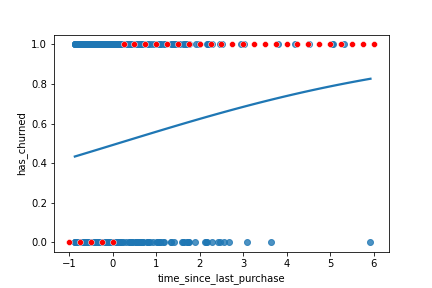
prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))

prediction_data["most_likely_outcome"] = np.round(prediction_data["has_churned"])

Visualizing most likely outcome

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="most_likely_outcome",
                data=prediction_data,
                color="red")

plt.show()

The scatter plot of churn versus time since last purchase, with a logistic trend line. The plot is annotated with the most likely outcomes. For low time since last purchase, the most likely outcome is not churning. For high time since last purchase, the most likely outcome is churning.

Odds ratios

Odds ratio is the probability of something happening divided by the probability that it doesn't.

$$ \text{odds\_ratio} = \frac{\text{probability}}{(1 - \text{probability)}} $$

$$ \text{odds\_ratio} = \frac{0.25}{(1 - 0.25)} = \frac{1}{3} $$

A line plot of odds ratio versus probability. The curve increases asymptotically to infinity as probability tends towards one.

Calculating odds ratio

prediction_data["odds_ratio"] = prediction_data["has_churned"] / 
                                (1 - prediction_data["has_churned"])

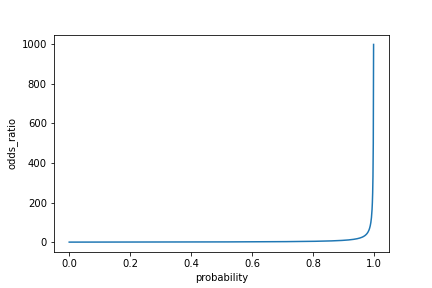
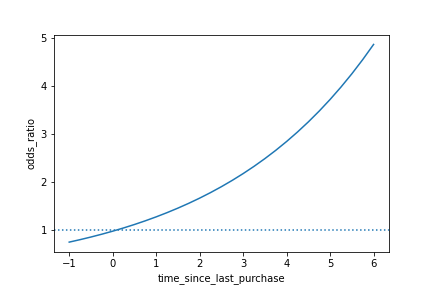
Visualizing odds ratio

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)


plt.axhline(y=1,
            linestyle="dotted")


plt.show()

A line plot of odds ratio versus time since last purchase, with a line at odds ratio equals one. For low time since last purchase, the most likely outcome is not churning. The odds of churning increase as time since last purchase increases, up to five time the odds of not churning.

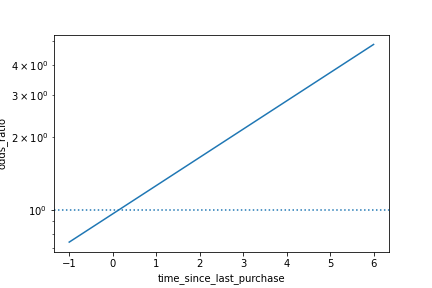
Visualizing log odds ratio

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)

plt.axhline(y=1,
            linestyle="dotted")

plt.yscale("log")

plt.show()

The line plot of odds ratio versus time since last purchase, with a line at odds ratio equals one. The y-axis uses a logarithmic scale, which has resulted in the odds ratio line becoming linear.

Calculating log odds ratio

prediction_data["log_odds_ratio"] = np.log(prediction_data["odds_ratio"])

All predictions together

time_since_last_prchs	has_churned	most_likely_rspns	odds_ratio	log_odds_ratio
0	0.491	0	0.966	-0.035
2	0.623	1	1.654	0.503
4	0.739	1	2.834	1.042
6	0.829	1	4.856	1.580
...	...	...	...	...

Comparing scales

Scale	Are values easy to interpret?	Are changes easy to interpret?	Is precise?
Probability	✔	✘	✔
Most likely outcome	✔✔	✔	✘
Odds ratio	✔	✘	✔
Log odds ratio	✘	✔	✔

Let's practice!

Introduction to Regression with statsmodels in Python