Predicting parallel slopes
Intermediate Regression with statsmodels in Python

Maarten Van den Broeck
Content Developer at DataCamp
The prediction workflow
import pandas as pd
import numpy as np
expl_data_length = pd.DataFrame(
{"length_cm": np.arange(5, 61, 5)})
print(expl_data_length)
length_cm
0 5
1 10
2 15
3 20
4 25
5 30
6 35
7 40
8 45
9 50
10 55
11 60
The prediction workflow
[A, B, C] x [1, 2] ==> [A1, B1, C1, A2, B2, C2]
from itertools import productproduct(["A", "B", "C"], [1, 2])
length_cm = np.arange(5, 61, 5)species = fish["species"].unique()p = product(length_cm, species)expl_data_both = pd.DataFrame(p, columns=['length_cm', 'species'])print(expl_data_both)
length_cm species
0 5 Bream
1 5 Roach
2 5 Perch
3 5 Pike
4 10 Bream
5 10 Roach
6 10 Perch
...
41 55 Roach
42 55 Perch
43 55 Pike
44 60 Bream
45 60 Roach
46 60 Perch
47 60 Pike
The prediction workflow
Predict mass_g from length_cm only
prediction_data_length = expl_data_length.assign(
mass_g = mdl_mass_vs_length.predict(expl_data)
)
Predict mass_g from both explanatory variables
prediction_data_both = expl_data_both.assign(
mass_g = mdl_mass_vs_both.predict(expl_data)
)
length_cm mass_g
0 5 -361.7277
1 10 -187.2315
2 15 -12.7353
3 20 161.7610
4 25 336.2572
5 30 510.7534
... # number of rows: 12
length_cm species mass_g
0 5 Bream -459.3991
1 5 Roach -513.9350
2 5 Perch -500.4501
3 5 Pike -876.6133
4 10 Bream -246.5563
5 10 Roach -301.0923
... # number of rows: 48
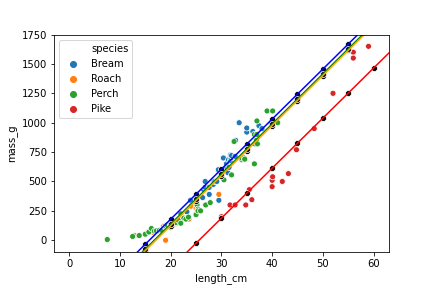
Visualizing the predictions
plt.axline(xy1=(0, ic_bream), slope=sl, color="blue")
plt.axline(xy1=(0, ic_perch), slope=sl, color="green")
plt.axline(xy1=(0, ic_pike), slope=sl, color="red")
plt.axline(xy1=(0, ic_roach), slope=sl, color="orange")
sns.scatterplot(x="length_cm",
y="mass_g",
hue="species",
data=fish)
sns.scatterplot(x="length_cm",
y="mass_g",
color="black",
data=prediction_data)
Manually calculating predictions for linear regression
coeffs = mdl_mass_vs_length.params
print(coeffs)
intercept, slope = coeffs
explanatory_data = pd.DataFrame(
{"length_cm": np.arange(5, 61, 5)})
prediction_data = explanatory_data.assign(
mass_g = intercept + slope * explanatory_data
)
print(prediction_data)
Intercept -536.223947
length_cm 34.899245
length_cm mass_g
0 5 -361.727721
1 10 -187.231494
2 15 -12.735268
3 20 161.760959
4 25 336.257185
5 30 510.753412
...
9 50 1208.738318
10 55 1383.234545
11 60 1557.730771
Manually calculating predictions for multiple regression
coeffs = mdl_mass_vs_both.params
print(coeffs)
species[Bream] -672.241866
species[Perch] -713.292859
species[Pike] -1089.456053
species[Roach] -726.777799
length_cm 42.568554
ic_bream, ic_perch, ic_pike, ic_roach, slope = coeffs
np.select()
conditions = [
condition_1,
condition_2,
# ...
condition_n
]
choices = [list_of_choices] # same length as conditions
np.select(conditions, choices)
Choosing an intercept with np.select()
conditions = [
explanatory_data["species"] == "Bream",
explanatory_data["species"] == "Perch",
explanatory_data["species"] == "Pike",
explanatory_data["species"] == "Roach"
]
choices = [ic_bream, ic_perch, ic_pike, ic_roach]
intercept = np.select(conditions, choices)
print(intercept)
[ -672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46
-672.24 -726.78 -713.29 -1089.46]
The final prediction step
prediction_data = explanatory_data.assign( intercept = np.select(conditions, choices), mass_g = intercept + slope * explanatory_data["length_cm"])print(prediction_data)
length_cm species intercept mass_g
0 5 Bream -672.2419 -459.3991
1 5 Roach -726.7778 -513.9350
2 5 Perch -713.2929 -500.4501
3 5 Pike -1089.4561 -876.6133
4 10 Bream -672.2419 -246.5563
5 10 Roach -726.7778 -301.0923
6 10 Perch -713.2929 -287.6073
7 10 Pike -1089.4561 -663.7705
8 15 Bream -672.2419 -33.7136
...
40 55 Bream -672.2419 1669.0286
41 55 Roach -726.7778 1614.4927
42 55 Perch -713.2929 1627.9776
43 55 Pike -1089.4561 1251.8144
44 60 Bream -672.2419 1881.8714
45 60 Roach -726.7778 1827.3354
46 60 Perch -713.2929 1840.8204
47 60 Pike -1089.4561 1464.6572
Compare to .predict()
mdl_mass_vs_both.predict(explanatory_data)
0 -459.3991
1 -513.9350
2 -500.4501
3 -876.6133
4 -246.5563
5 -301.0923
...
43 1251.8144
44 1881.8714
45 1827.3354
46 1840.8204
47 1464.6572
Let's practice!
Intermediate Regression with statsmodels in Python

