Measures of spread

Statistical Techniques in Tableau

Maarten Van den Broeck

Content Developer at DataCamp

Statistics for describing a variable

Statistic	Description
Count	number of observations
Median	midpoint of your observations
Average	mean value of your observations
Min/Max	lowest and highest value
Quartile/IQR	25th and 75th percentile / spread of the 50% of your middlemost observations
Modality/Mode	number of modes / most occurring value
Skewness	(a)symmetry of the distribution
Kurtosis	distribution of extreme values

Measures of spread

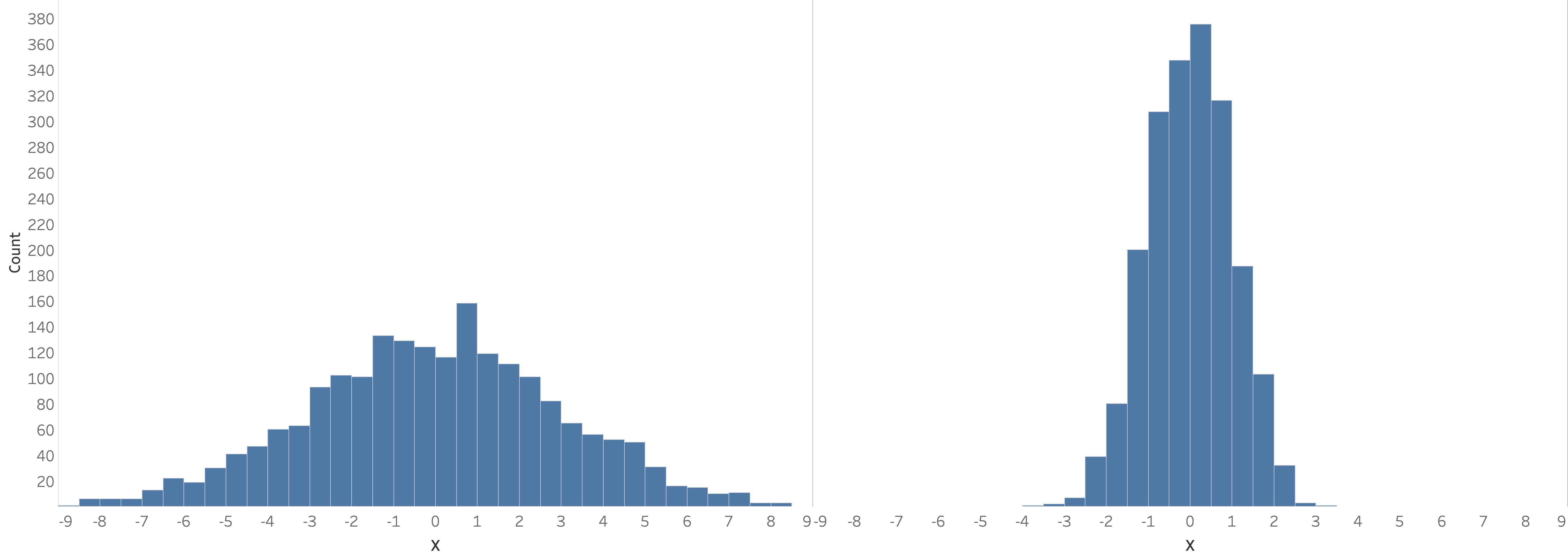
Two normally distributed histograms, with different variances

Spread is affected by kurtosis (outliers) and skewness (asymmetry)
Typically, spread around the mean is only useful for normal distributions

Variance

$x_{i} - \overline{x}$

$(x_{i} - \overline{x})^2$

$\sum(x_{i} - \overline{x})^2$

$\frac{\sum(x_{i} - \overline{x})^2}{n - 1}$

Variance is the average of the squared differences from the mean
Higher variance means higher spread of the data
Unit of variance is squared

$x_i$ = individual data point, $\overline{x}$ = sample mean

$n$ = number of observations

¹ Note: you don't need to memorize the formulas. They unveil the black box of Tableau's calculations.

Standard deviation (SD or $s$)

$s = \sqrt{\frac{\sum(x_{i} - \overline{x})^2}{n - 1}}$ or $s = \sqrt{variance}$

Unit of standard deviation is same as the variable
How far on average lie the data points from the mean
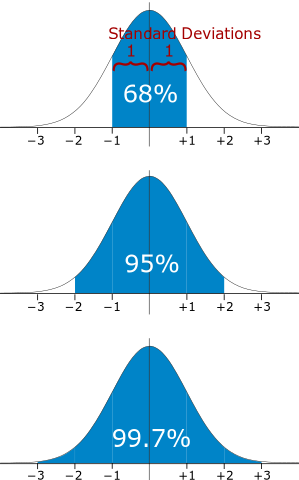
68% of the observations lies within $[-1s, 1s]$ range if data is normally distributed
Number of standard deviations can be used as a threshold to pinpoint unusual values

A normal distribution with different standard deviation levels.

Population vs. sample

Representation of a freshwater lake, with its species distribution. All species are considered as the population.

Population vs. sample

Taking a subset from a population is called sampling.

Population vs. sample

Inference: the process of making statements about the population from the sample.

Calculating spread in sample vs. population

Sample variance $s^2$

$s^2 = \frac{\sum(x_{i} - \overline{x})^2}{n - 1}$

data per country (sample) generalize for Europe (population)

Sample standard deviation $s$

$s = \sqrt{\frac{\sum(x_{i} - \overline{x})^2}{n - 1}}$ $\overline{x}$ = sample mean

$n$ = sample size

Population variance $\sigma$

$\sigma^2 = \frac{\sum(x_{i} - \mu)^2}{N}$

data of your university (population) no need for generalizing

Population standard deviation $\sigma^2$

$\sigma = \sqrt{\frac{\sum(x_{i} - \mu)^2}{N}}$ $\mu$ = population mean

$N$ = population size

¹ Note: you don't need to memorize the formulas. They unveil the black box of Tableau's calculations.

Calculating spread in sample vs. population

Sample variance $s^2$

$s^2 = \frac{\sum(x_{i} - \overline{x})^2}{\textbf{n - 1}}$

data per country (sample) generalize for Europe (population)

Sample standard deviation $s$

$s = \sqrt{\frac{\sum(x_{i} - \overline{x})^2}{\textbf{n - 1}}}$ $\overline{x}$ = sample mean

$n$ = sample size

Population variance $\sigma^2$

$\sigma^2 = \frac{\sum(x_{i} - \mu)^2}{\textbf{N}}$

data of your university (population) no need for generalizing

Population standard deviation $\sigma$

$\sigma = \sqrt{\frac{\sum(x_{i} - \mu)^2}{\textbf{N}}}$ $\mu$ = population mean

$N$ = population size

¹ Note: you don't need to memorize the formulas. They unveil the black box of Tableau's calculations.

Let's practice!

Statistical Techniques in Tableau