The basics of linear regression

Supervised Learning with scikit-learn

George Boorman

Core Curriculum Manager, DataCamp

Regression mechanics

$y = ax + b$
- Simple linear regression uses one feature
  - $y$ = target
  - $x$ = single feature
  - $a$, $b$ = parameters/coefficients of the model - slope, intercept
How do we choose $a$ and $b$?
- Define an error function for any given line
- Choose the line that minimizes the error function
Error function = loss function = cost function

The loss function

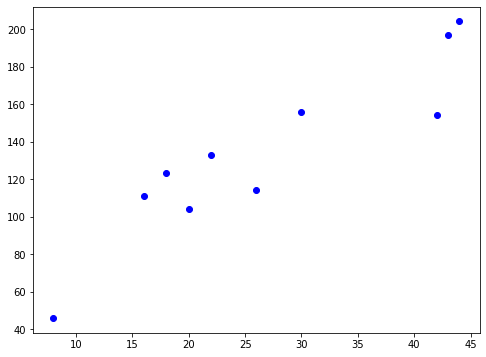
scatter plot

The loss function

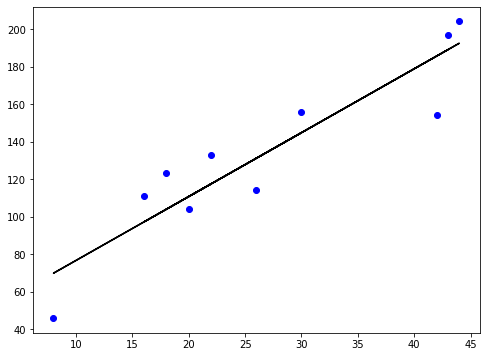
regression line running from bottom left to top right, through the middle of the observations

The loss function

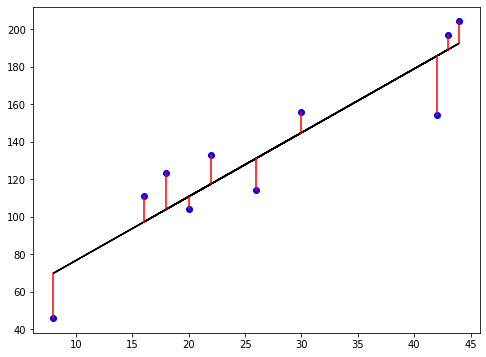
red lines from the regression line to each observation

The loss function

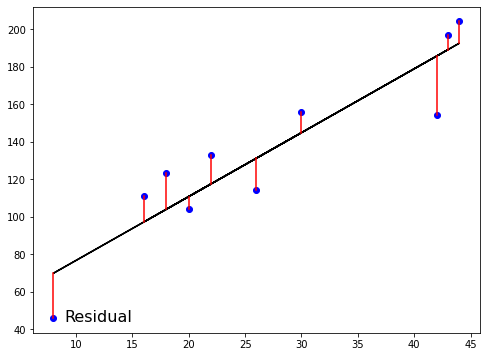
the red lines represent residuals

The loss function

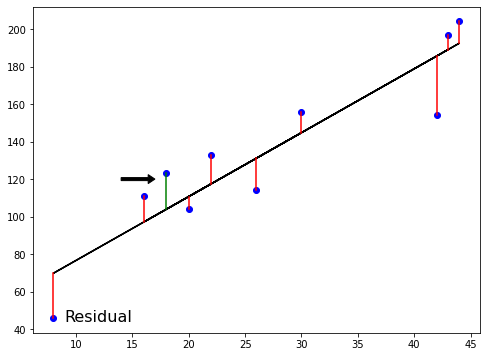
arrow highlighting a postive arrow, as the observation is above the regression line

Ordinary Least Squares

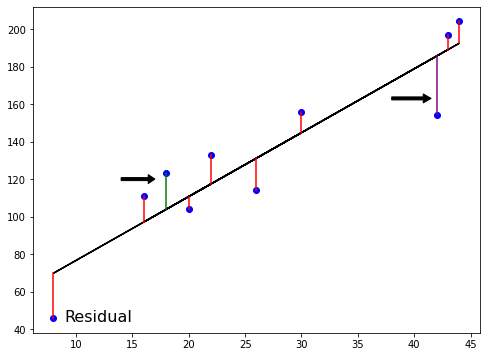
second arrow pointing to a residual beneath the regression line, representing a negative residual

$RSS = $ $\displaystyle\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

Ordinary Least Squares (OLS): minimize RSS

Linear regression in higher dimensions

$$ y = a_{1}x_{1} + a_{2}x_{2} + b$$

To fit a linear regression model here:
- Need to specify 3 variables: $ a_1,\ a_2,\ b $
In higher dimensions:
- Known as multiple regression
- Must specify coefficients for each feature and the variable $b$

$$ y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} +... + a_{n}x_{n}+ b$$

scikit-learn works exactly the same way:
- Pass two arrays: features and target

Linear regression using all features

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                    random_state=42)

reg_all = LinearRegression()

reg_all.fit(X_train, y_train)

y_pred = reg_all.predict(X_test)

R-squared

$R^2$: quantifies the variance in target values explained by the features
- Values range from 0 to 1
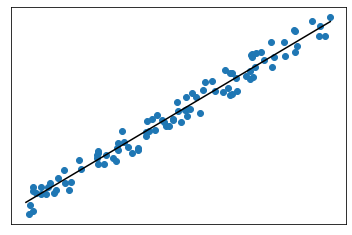
High $R^2$:

regression line at 45 degrees running from bottom left to top right and close to all the observations

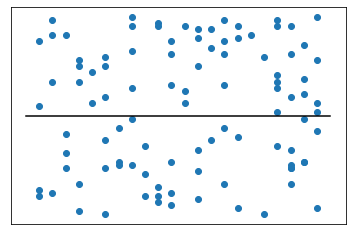
Low $R^2$:

regression line running horizontally, where observations are spread out away from the line

R-squared in scikit-learn

reg_all.score(X_test, y_test)

0.356302876407827

Mean squared error and root mean squared error

$MSE = $ $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

$MSE$ is measured in target units, squared

$RMSE = $ $\sqrt{MSE}$

Measure $RMSE$ in the same units at the target variable

RMSE in scikit-learn

from sklearn.metrics import mean_squared_error

mean_squared_error(y_test, y_pred, squared=False)

24.028109426907236

Let's practice!

Supervised Learning with scikit-learn