The binomial distribution
Introduction to Statistics

George Boorman
Curriculum Manager, DataCamp
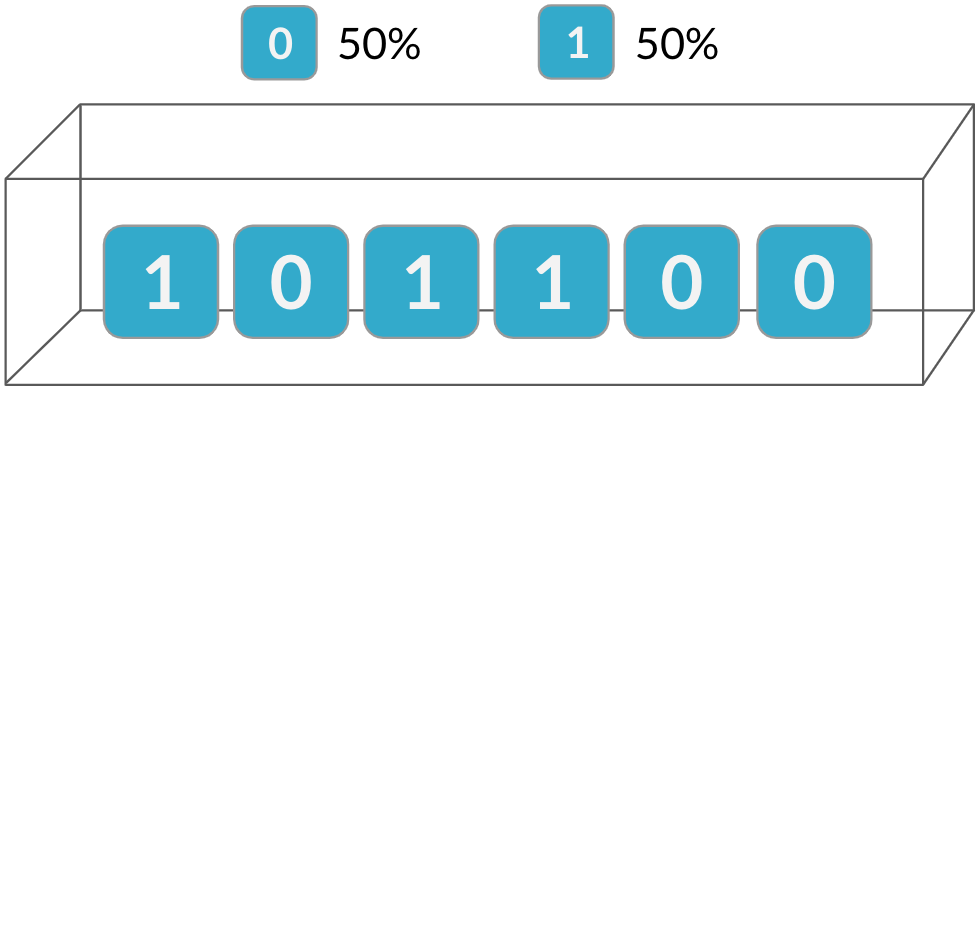
Coin flipping
Binary outcomes
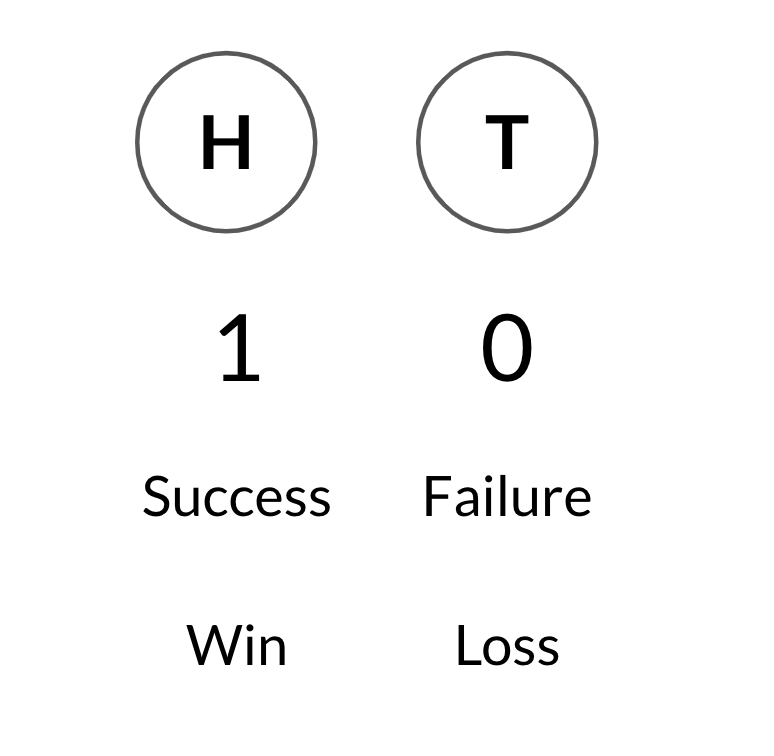
One coin flip many times
| Coin Flip | Result |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
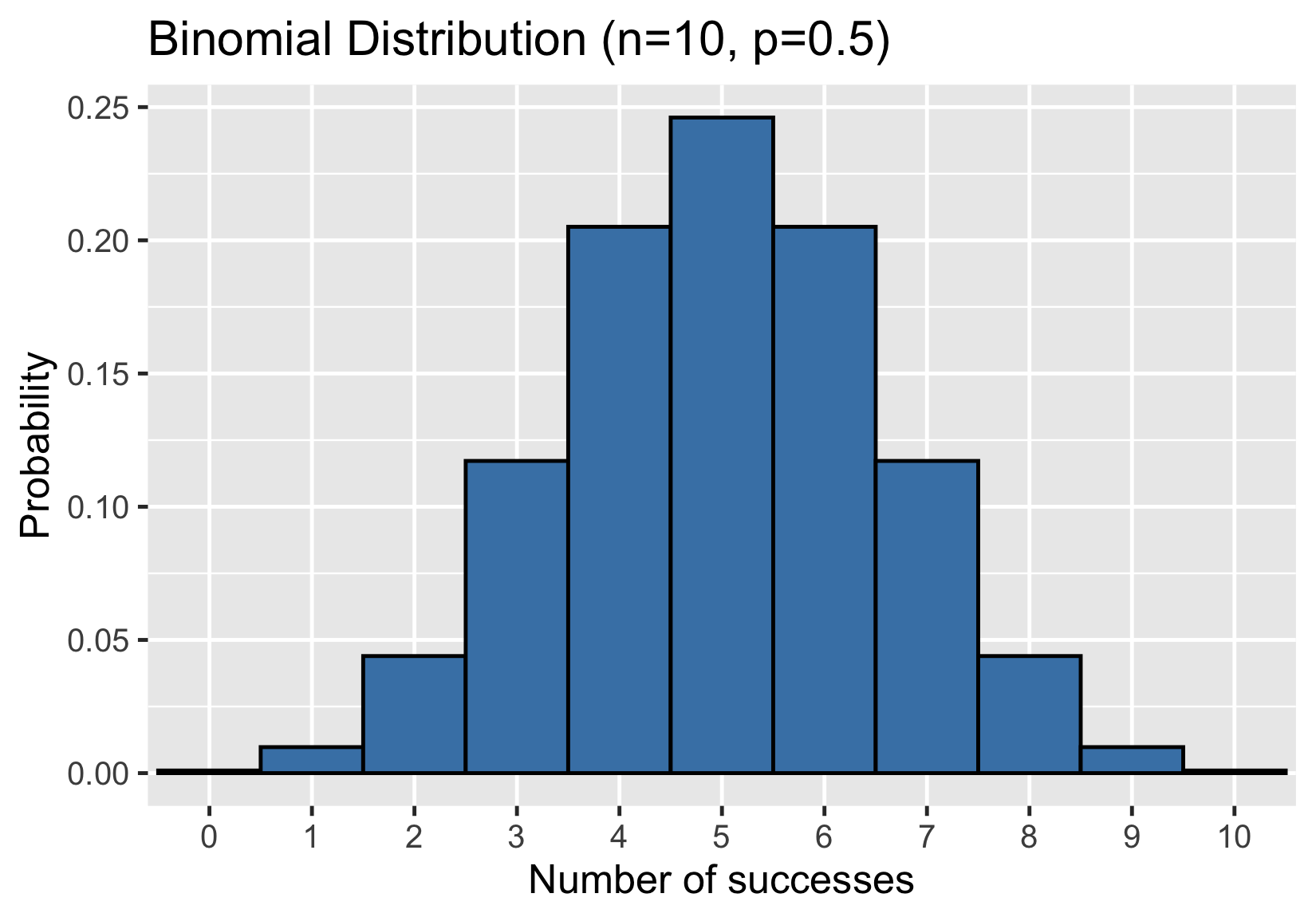
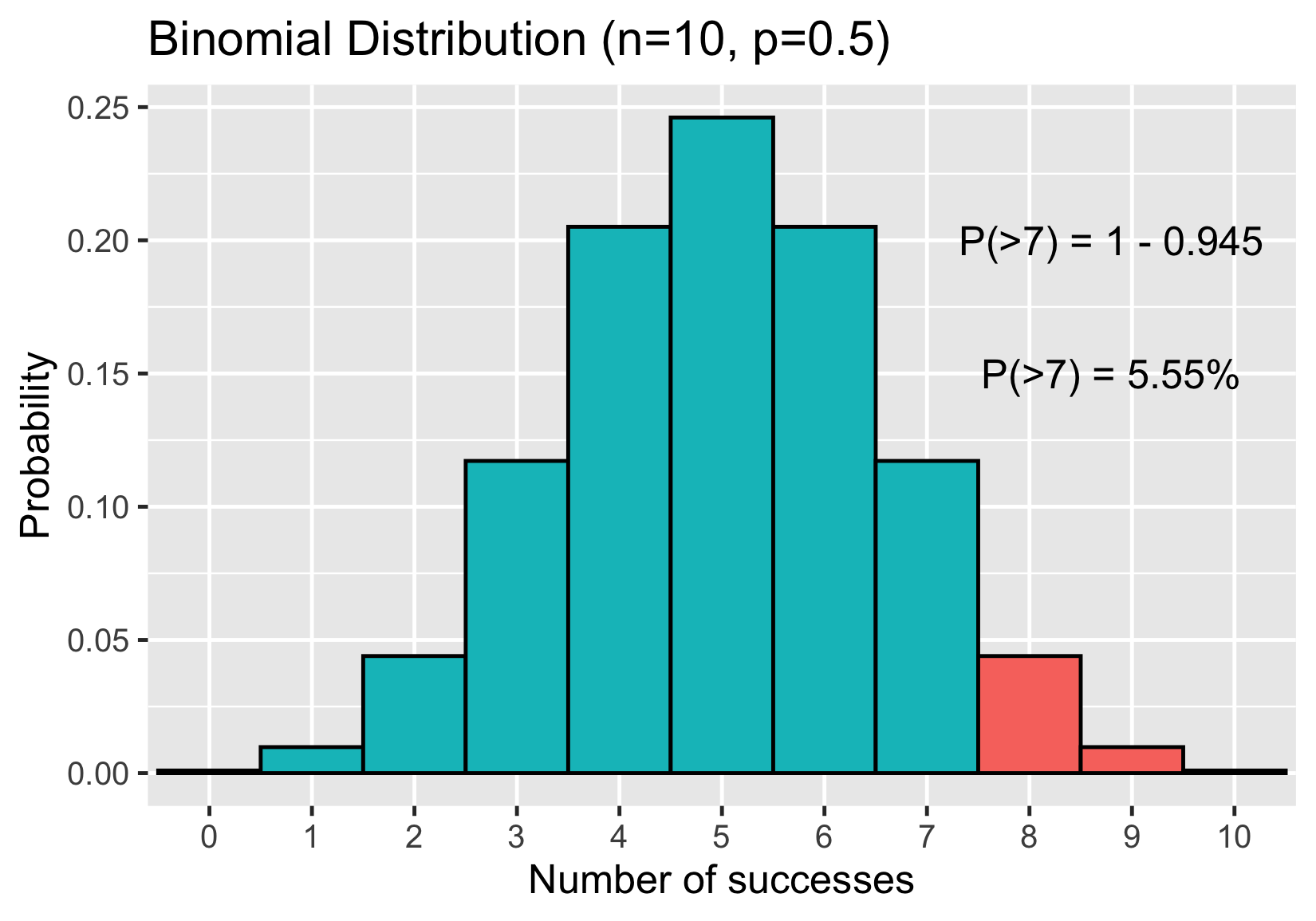
Binomial distribution
Probability distribution of the number of successes in a sequence of independent events
For example, the number of heads in a sequence of coin flips
Described by $n$ and $p$
- $n$: total number of events
- $p$: probability of success
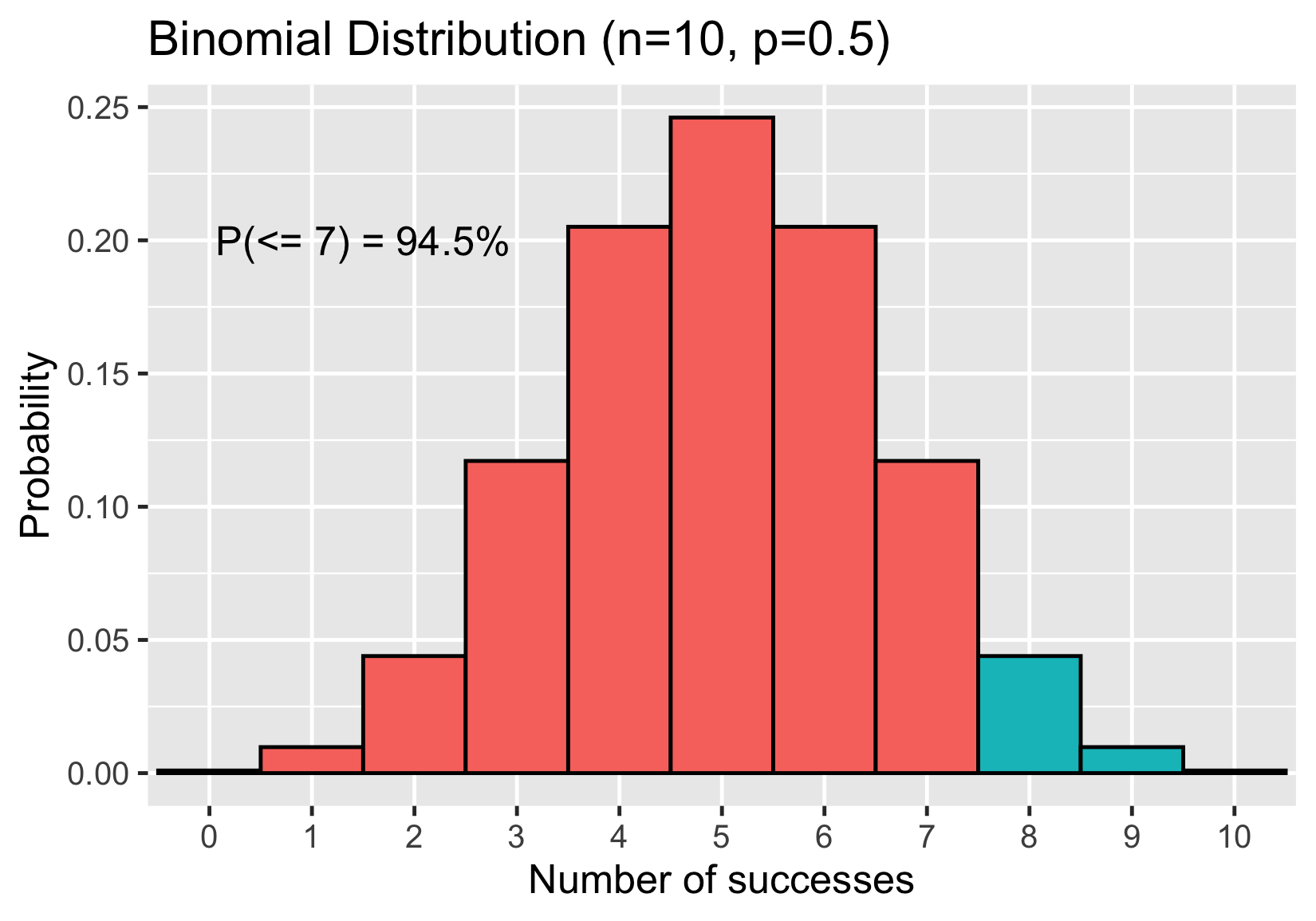
Binomial distribution
Probability of 7 or fewer heads
Probability of 8 or more heads
Expected value
${Expected \ value} = n \times p$
Expected number of heads out of 10 flips $= 10 \times 0.5 = 5$
If we don't know $p$, but know $n$ and the expected value:
${p} = \frac{expected \ value}{n} $
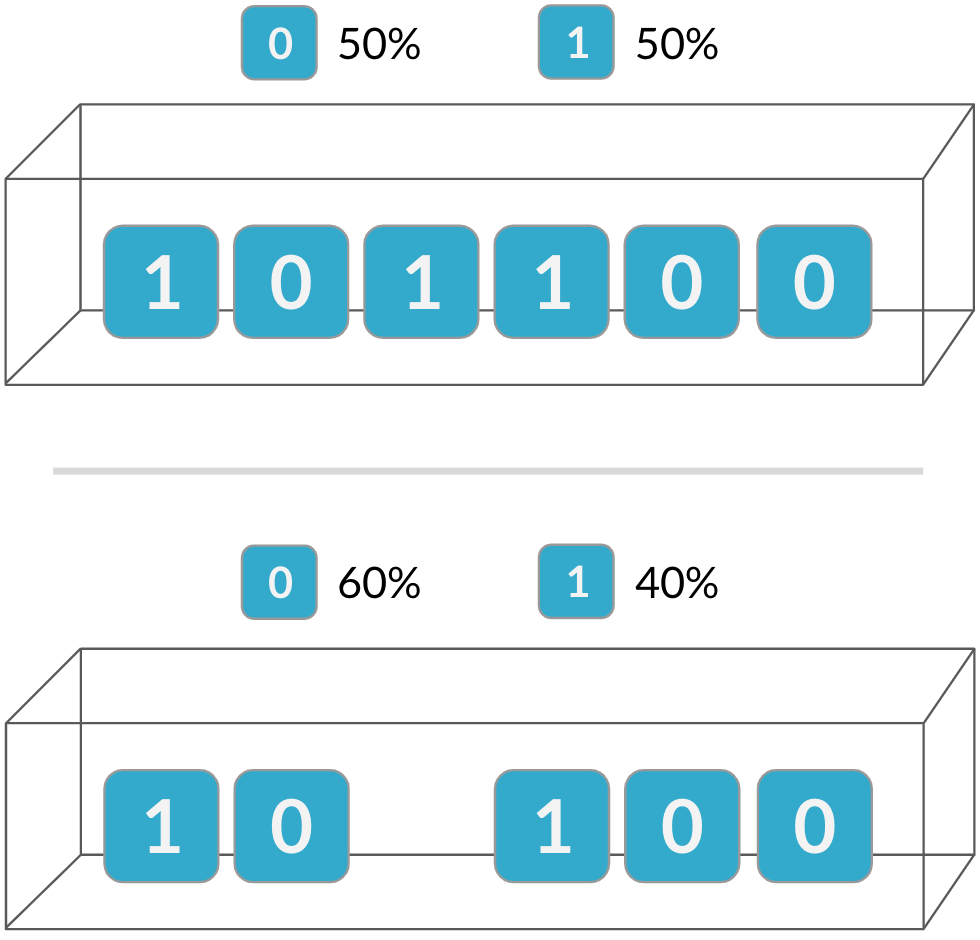
Independence
The binomial distribution is a probability distribution of the number of successes in a sequence of independent events
Independence
The binomial distribution is a probability distribution of the number of successes in a sequence of independent events
Probabilities of second event are altered due to outcome of the first
If events are not independent, the binomial distribution does not apply!
General applications
The binomial distribution can be used for independent events producing binary outcomes
- Clinical trial measuring drug effectiveness
- Effective or not
- Betting on the result of a sports match
- Bettor can win or lose

Let's practice!
Introduction to Statistics

