Discrete distributions

Introduction to Statistics

George Boorman

Curriculum Manager, DataCamp

Six-sided die.png

Introduction to Statistics

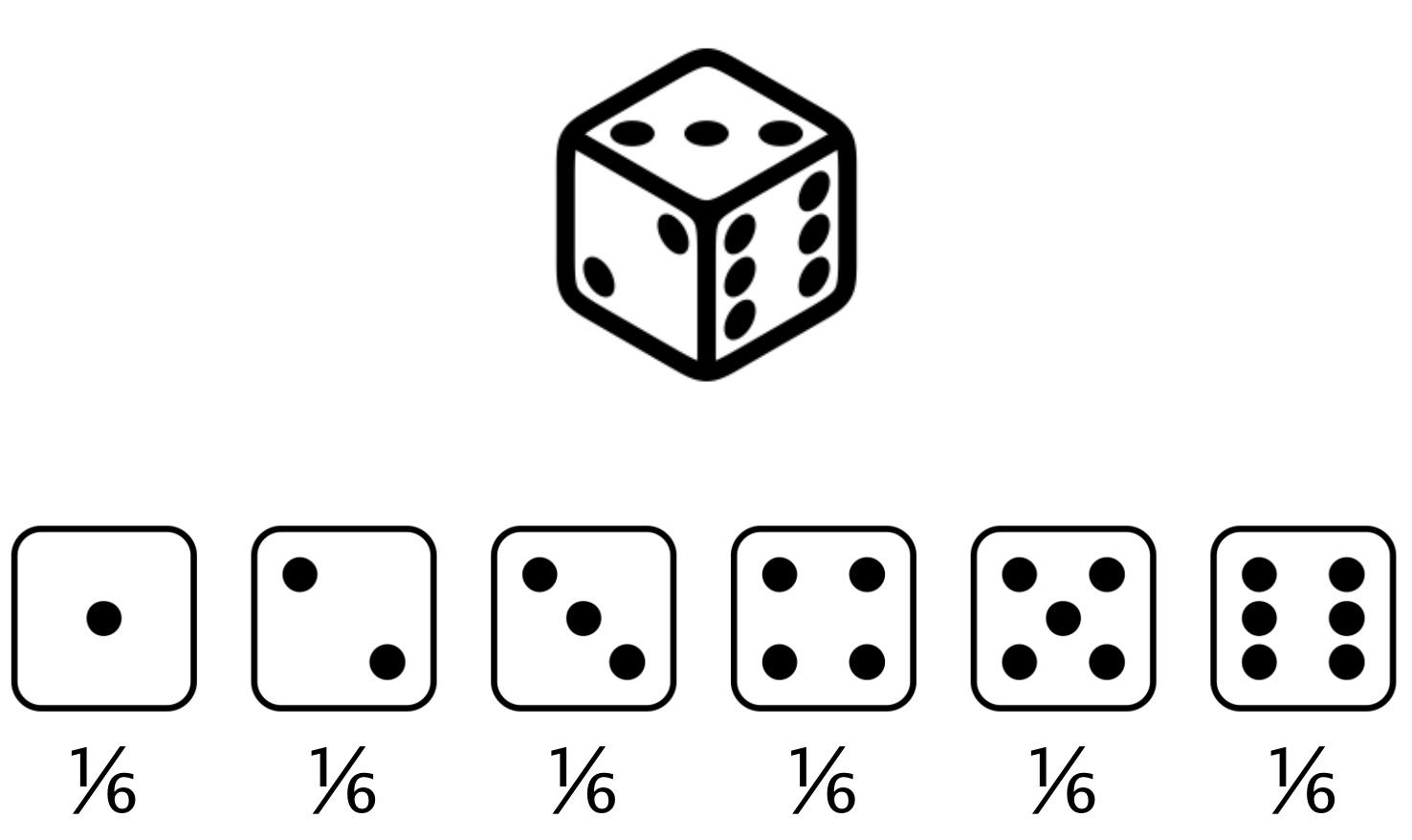
Rolling the dice

Each side of a die has 1/6 probability.png

Introduction to Statistics

Choosing salespeople

 

Names in a box, each with 25% probability.png

Introduction to Statistics

Probability distribution

Describes the probability of each possible outcome in a scenario

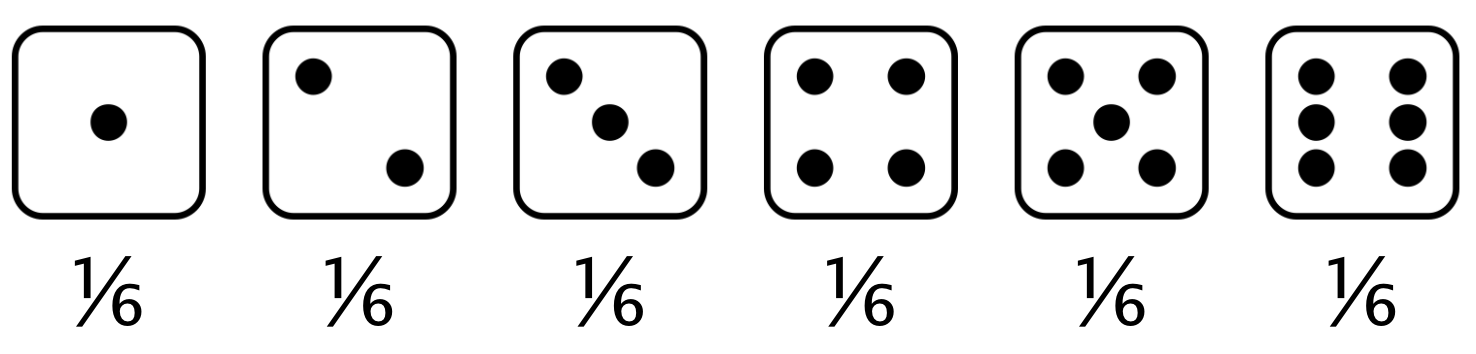
Each side of a die has 1/6 probability.png

 

Expected value: The mean of a probability distribution

Expected value of a fair die roll = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.5$

Introduction to Statistics

Why are probability distributions important?

  • Help us to quantify risk and inform decision making

 

 

  • Used extensively in hypothesis testing
    • Probability that the results occurred by chance

graffiti_on_a_wall_asking_what_now.jpg

1 Image credit: https://unsplash.com/@timmossholder
Introduction to Statistics

Visualizing a probability distribution

Histogram_with_a_bar_for_each_number_one_through_six_with_height_one_sixth_each.png

Introduction to Statistics

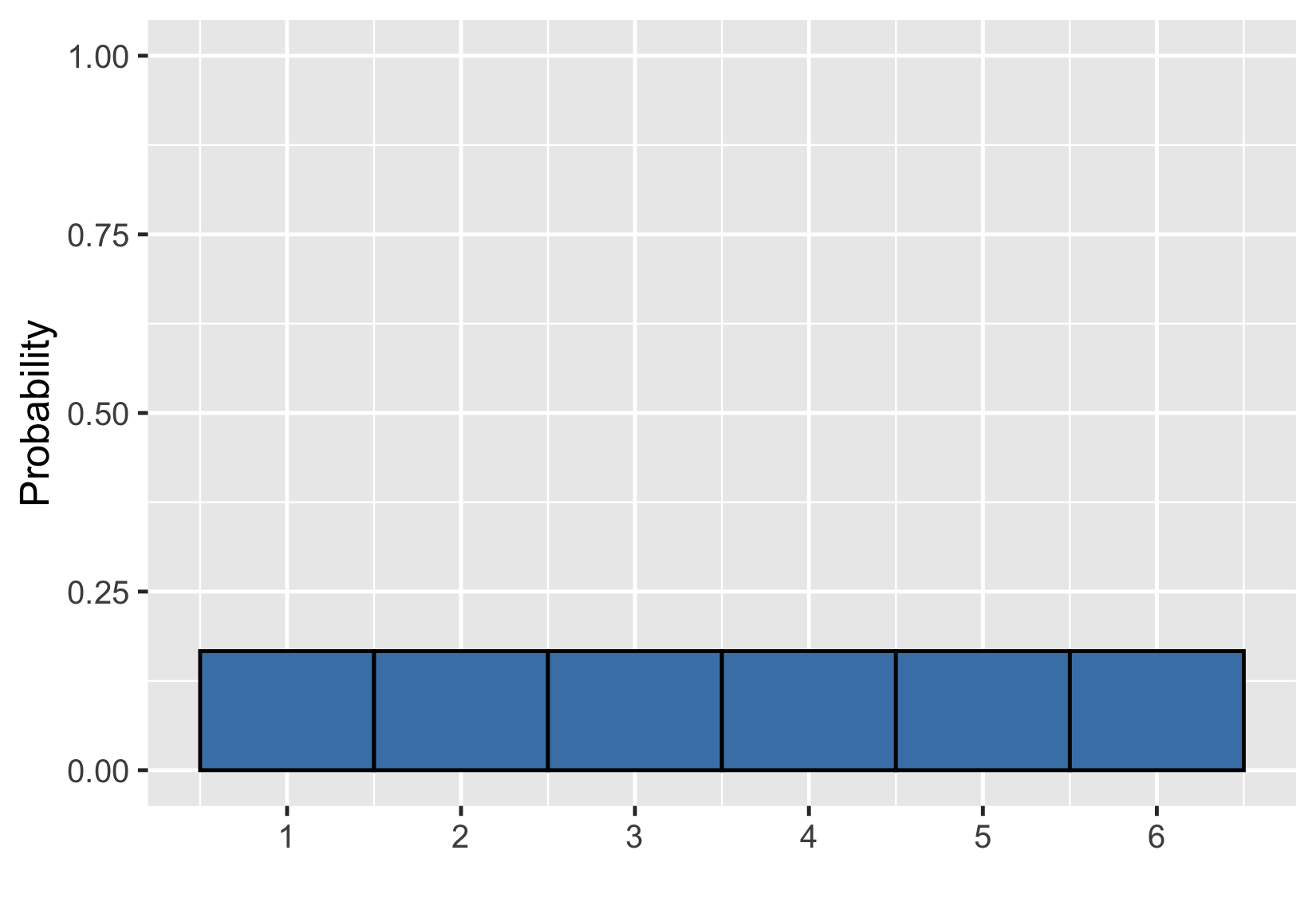
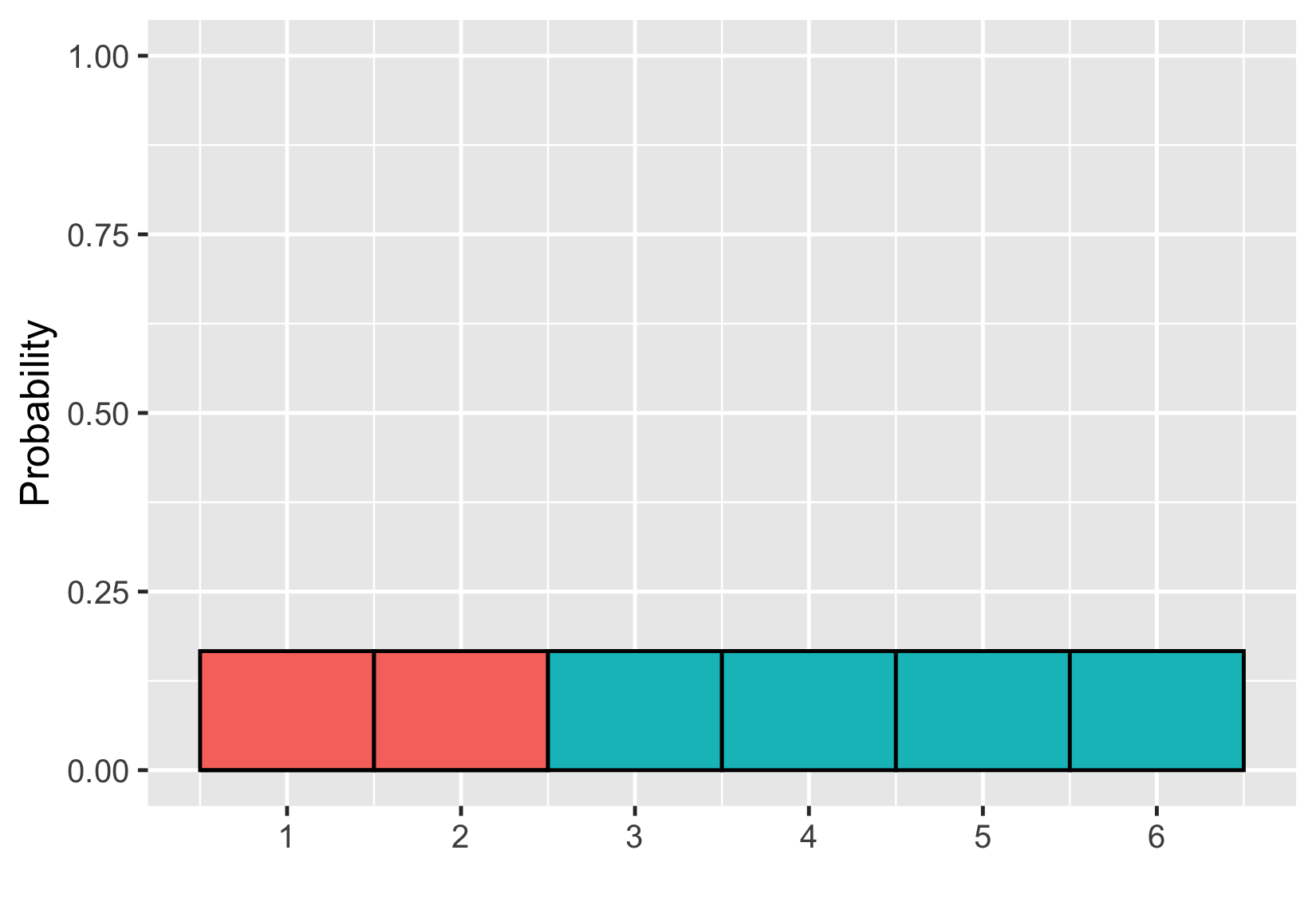
Probability = area

$$P(\text{die roll}) \le 2 = ~?$$

bars_for_one_and_two_highlighted.png

Introduction to Statistics

Probability = area

$$P(\text{die roll}) \le 2 = 1/3$$

one_sixth_plus_one_sixth_equals_one_third.png

Introduction to Statistics

Uneven die

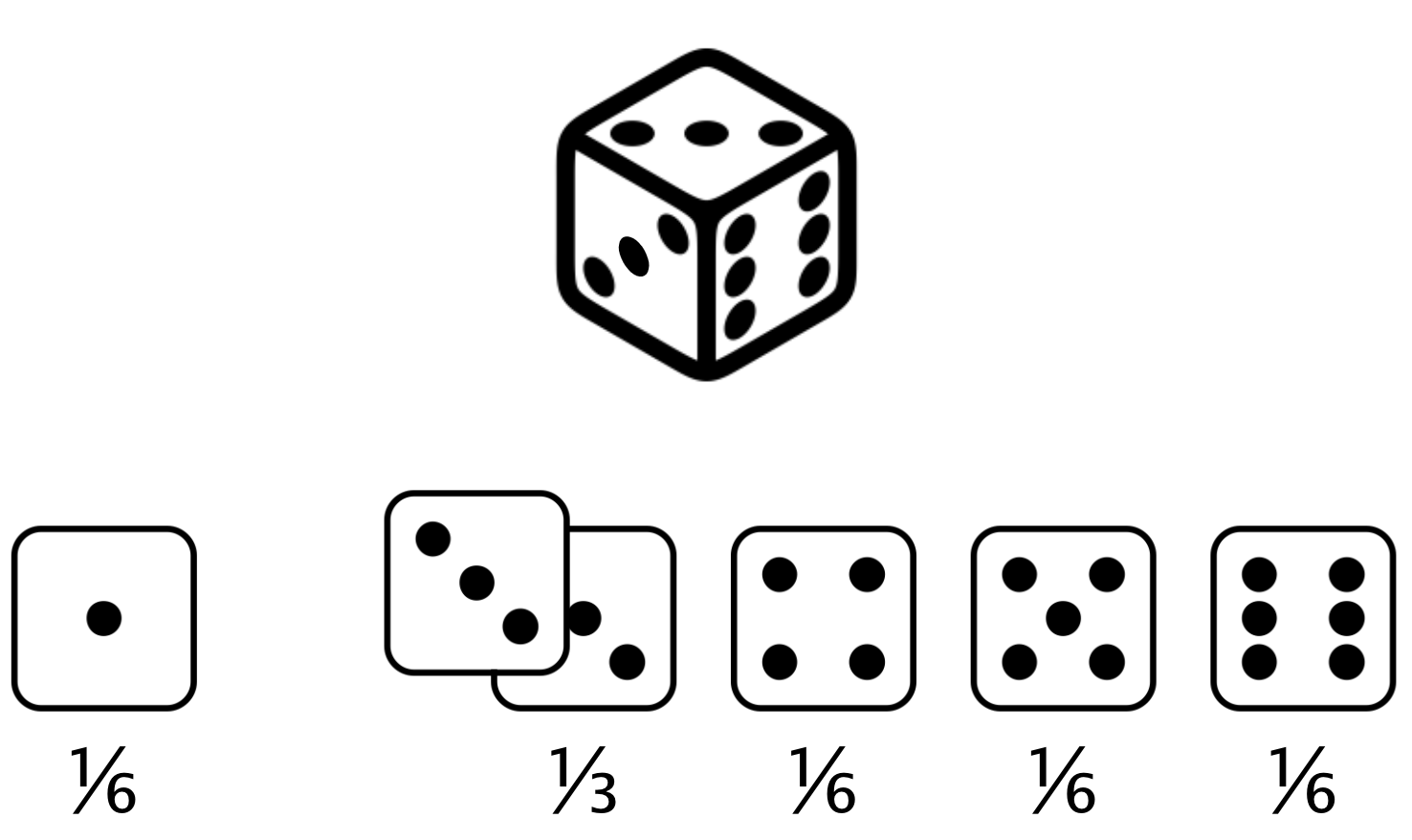
six-sided_die with_two_sides_with_three_dots.png

Expected value of uneven die roll = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.67$

Introduction to Statistics

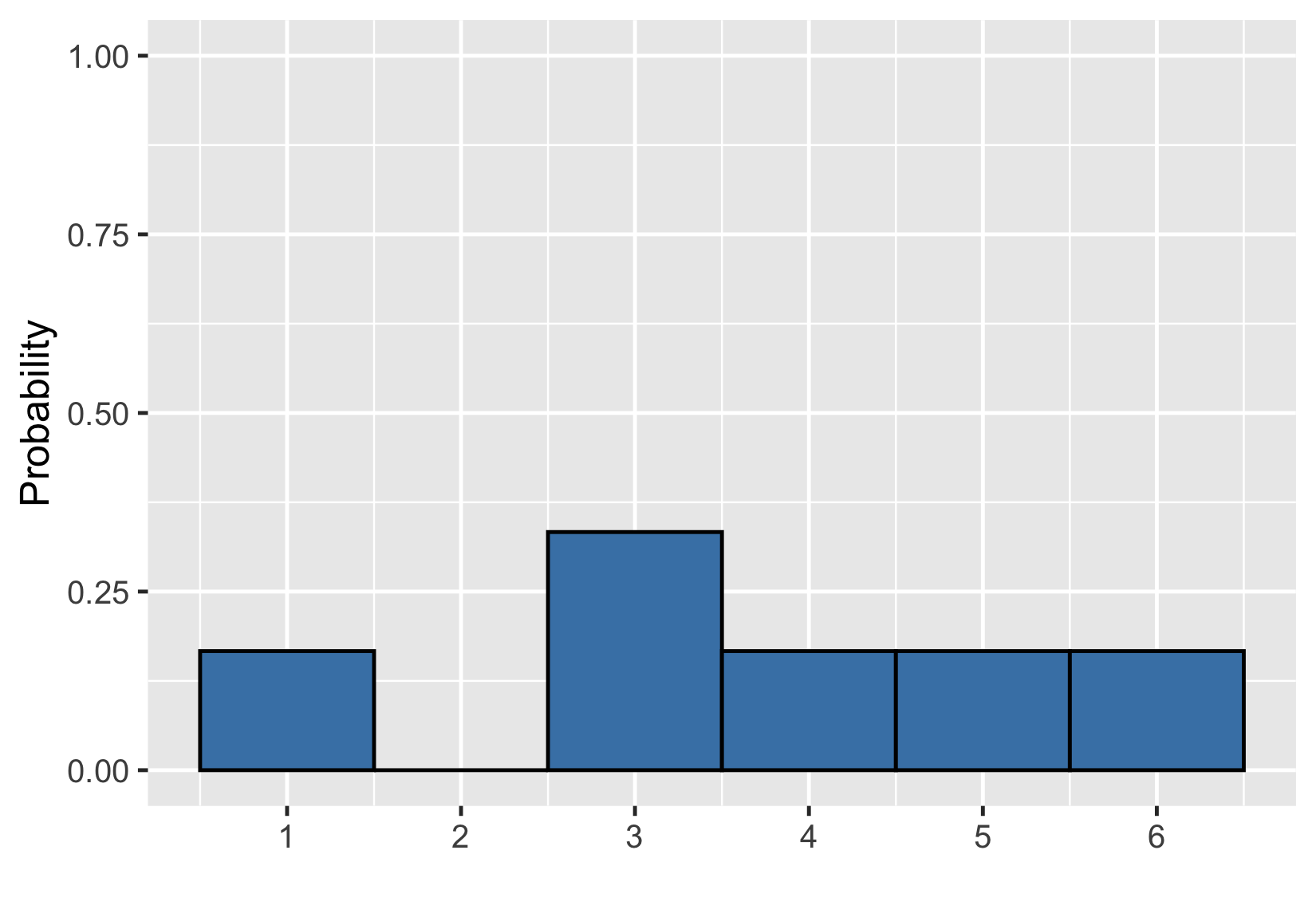
Visualizing uneven probabilities

Probability_distribution_of_uneven_die_with_bars_for_one_four_five_six_are height_one_sixth_bar_for_two_is_height_zero_bar_for_three_is_height_one_third.png

Introduction to Statistics

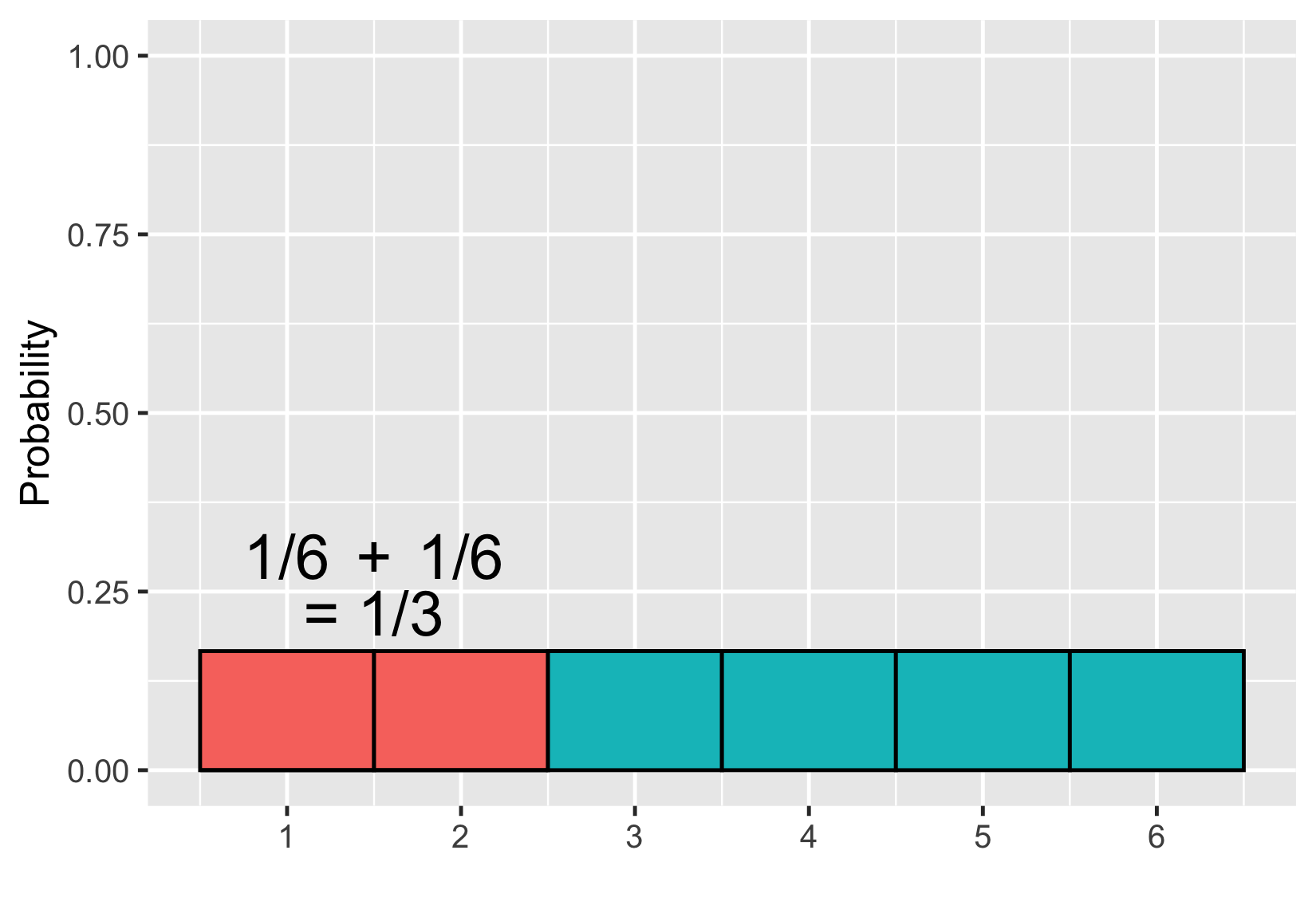
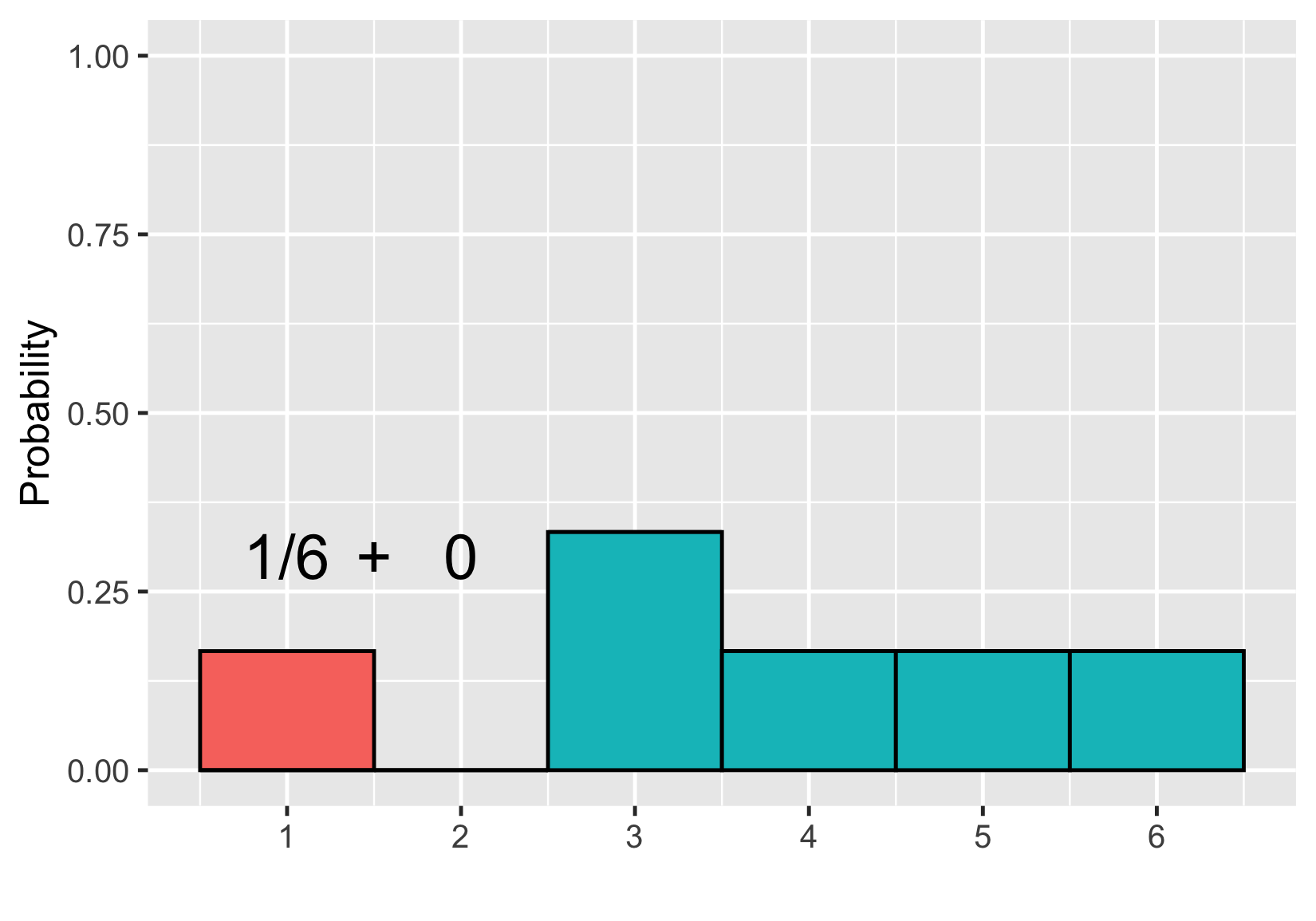
Adding areas

$$P(\text{uneven die roll}) \le 2 = ~?$$

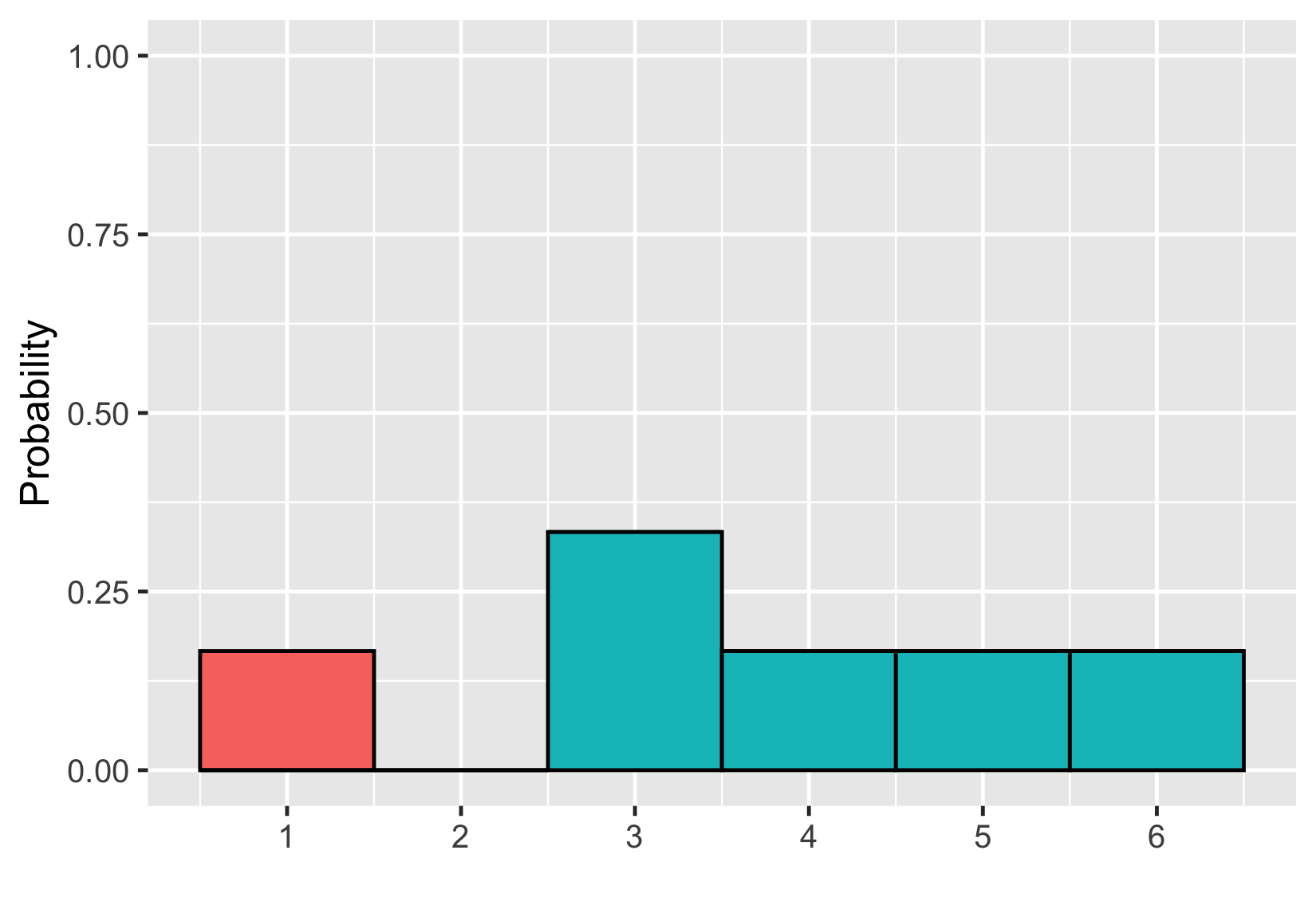
probability_distribution_with_one_highlighted.png

Introduction to Statistics

Adding areas

$$P(\text{uneven die roll}) \le 2 = 1/6$$

probability_distribution_with_text_stating_one_sixth_plus_zero.png

Introduction to Statistics

Discrete probability distributions

Describe probabilities for discrete outcomes

Fair die

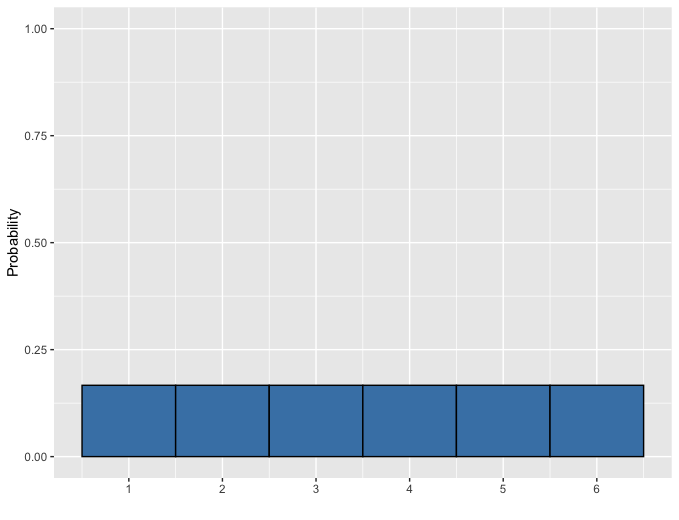
fair_dice_frequency distribution.png

                Discrete uniform distribution

 

Uneven die

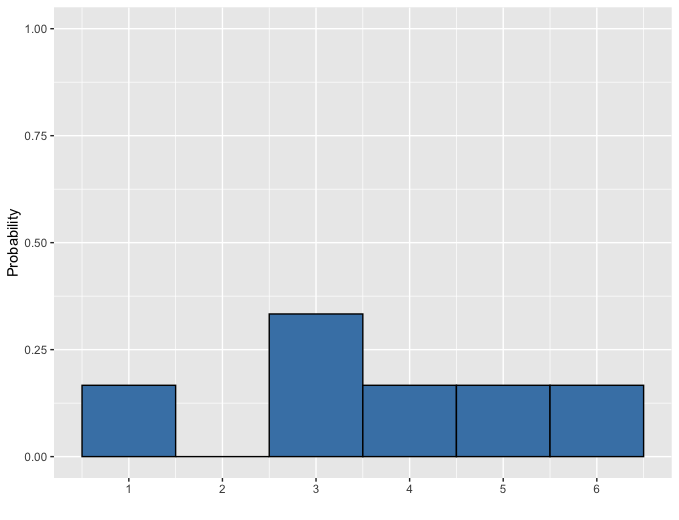
uneven_dice_frequency_distribution.png

Introduction to Statistics

Sampling from a discrete distribution

Roll Result
1 1
2 2
3 3
4 4
5 5
6 6

 

$ {Mean} = 3.5 $

Roll Result
1 3
2 1
3 2
4 4
5 6
6 3
7 2
8 2
9 2
10 5
Introduction to Statistics

Visualizing a sample

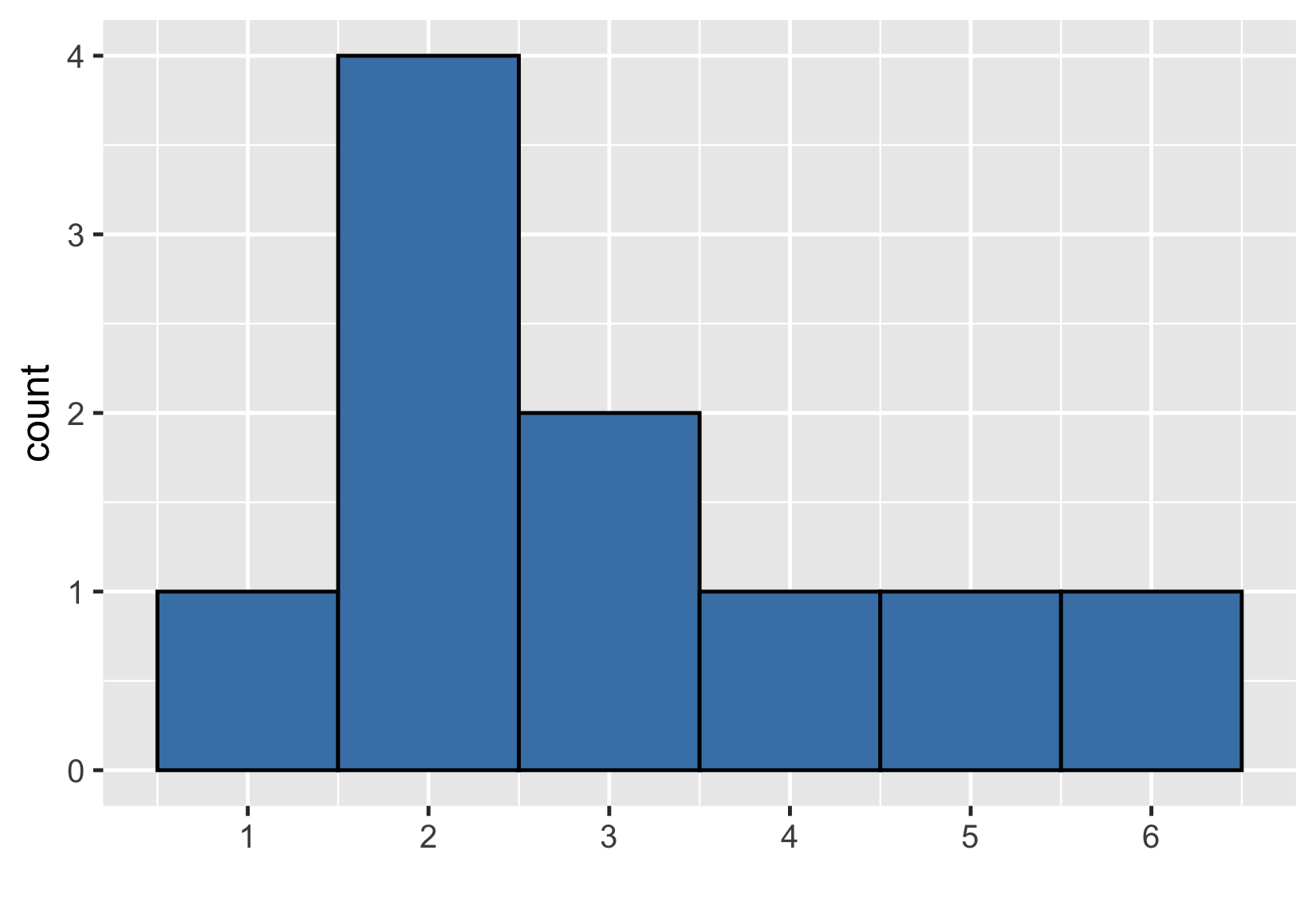
histogram_of_10_die_rolls.png

Introduction to Statistics

Sample distribution vs theoretical distribution

histogram_of_10_die_rolls.png

                            $ {Mean} = 3.0 $

even_dice_frequency_distribution.png

                            $ {Mean} = 3.5 $

Introduction to Statistics

A bigger sample

Sample of 100 rolls

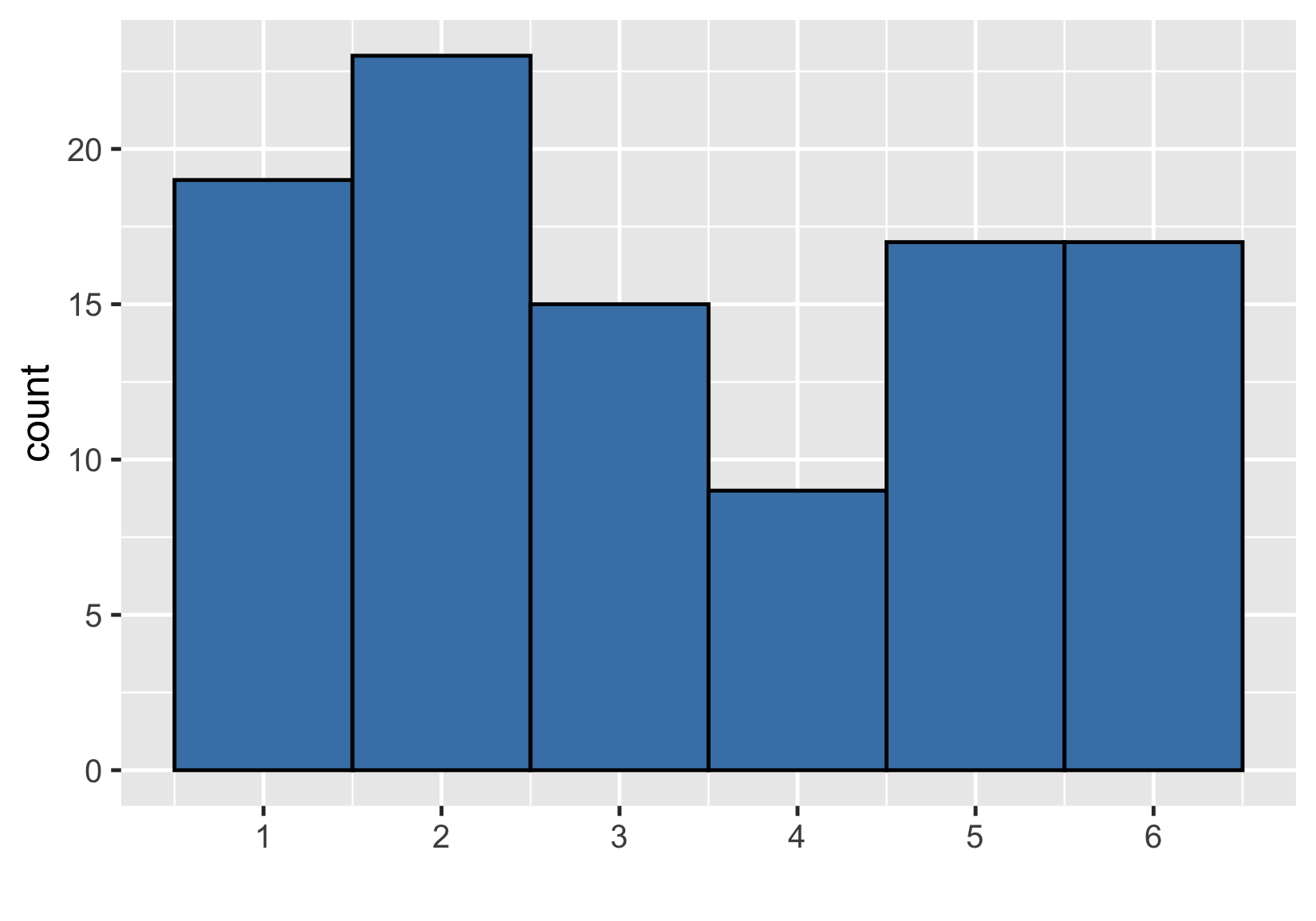
histogram_of_100_rolls.png

                                                                  $ {Mean} = 3.33 $

Introduction to Statistics

An even bigger sample

Sample of 1000 rolls

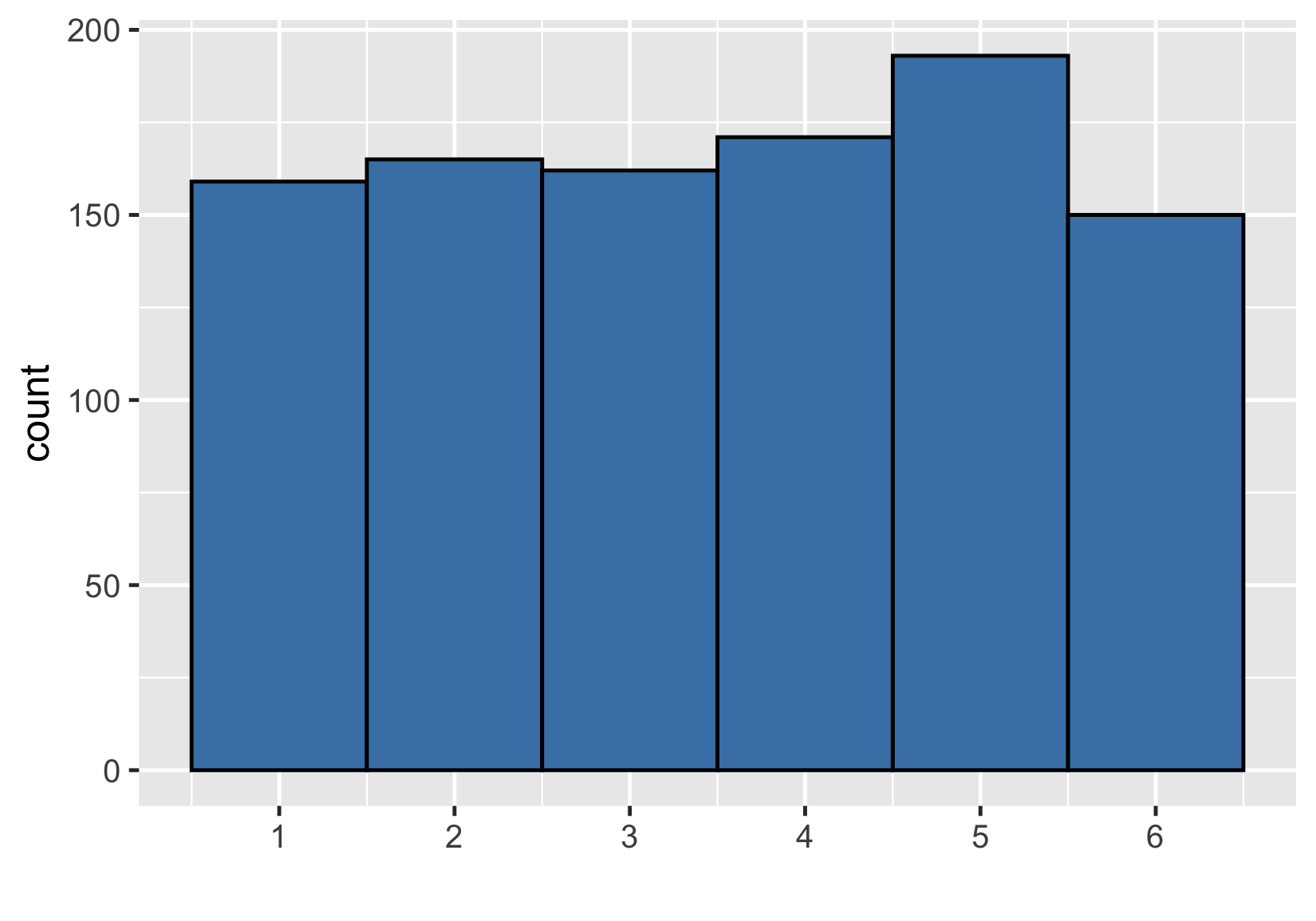
histogram_of_1000_rolls.png

                                                                  $ {Mean} = 3.52 $

Introduction to Statistics

Law of large numbers

As the size of your sample increases, the sample mean will approach the expected value.

Sample size Mean
10 3.00
100 3.33
1000 3.52
Introduction to Statistics

Let's practice!

Introduction to Statistics

Preparing Video For Download...