What are the chances?

Introduction to Statistics

George Boorman

Curriculum Manager, DataCamp

Measuring chance

What's the probability of an event?

$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$

Example: a coin flip

$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

line of probability from left where 0 percent = impossible, to right where 100 percent = will certainly happen.png

Box with Amir, Brian, Claire, and Damian's names.png

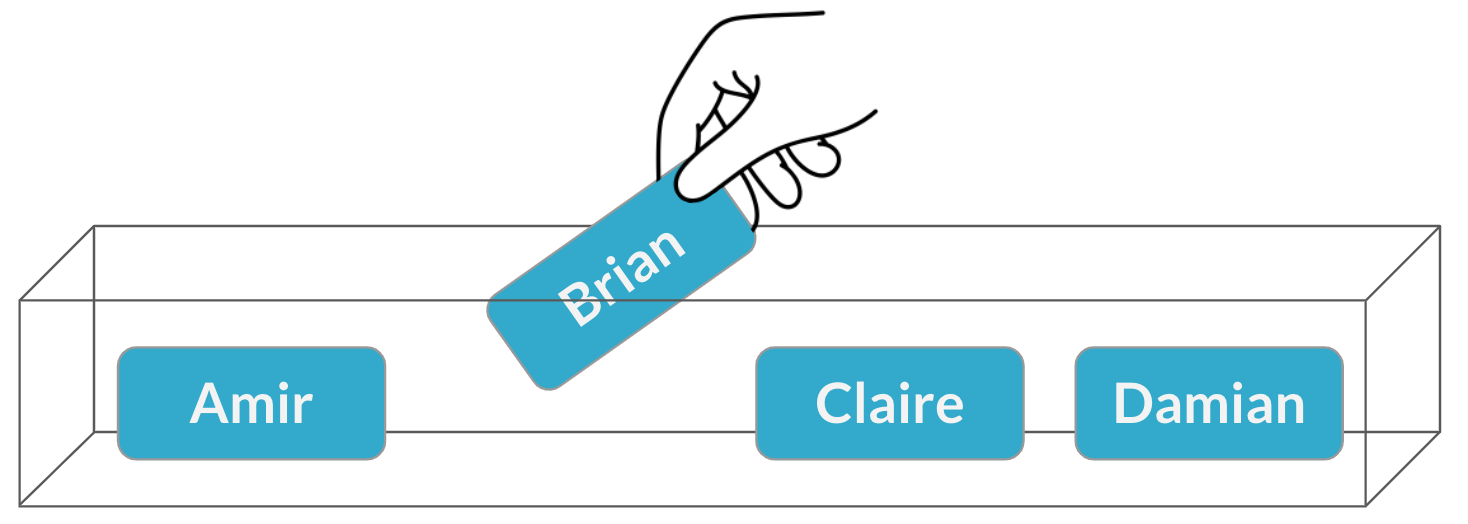
Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Pulling out Brian's name from the box.png

Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Two events are independent if the probability of the second event does not change based on the outcome of the first event.

Order Number	Product Type	Net Quantity	Gross Sales	Discounts	Returns	Net Sales
200	Basket	13	3744.0	-316.80	0.00	3427.20
201	Basket	12	3825.0	-201.60	-288.0	3335.40
202	Basket	17	3035.0	-63.25	0.00	2971.75
203	Art & Sculpture	47	2696.8	-44.16	0.00	2652.64
204	Basket	17	2695.0	-52.50	-110.00	2532.50

¹ Image credit: https://unsplash.com/@rodriguezedm

$$P(Jewelry) = \frac{Order \ Count(Jewelry)}{Sum(Total \ Order \ Count)}$$

$$P(Jewelry) = \frac{210}{1767}$$

$$P(Jewelry) = 11.88 \%$$

Introduction to Statistics