Understanding Big O Notation

Data Structures and Algorithms in Python

Miriam Antona

Software Engineer

Big O Notation

Measures the worst-case complexity of an algorithm
- Time complexity: time taken to run completely
- Space complexity: extra memory space
Doesn't use seconds/bytes
- Different results depending on the hardware
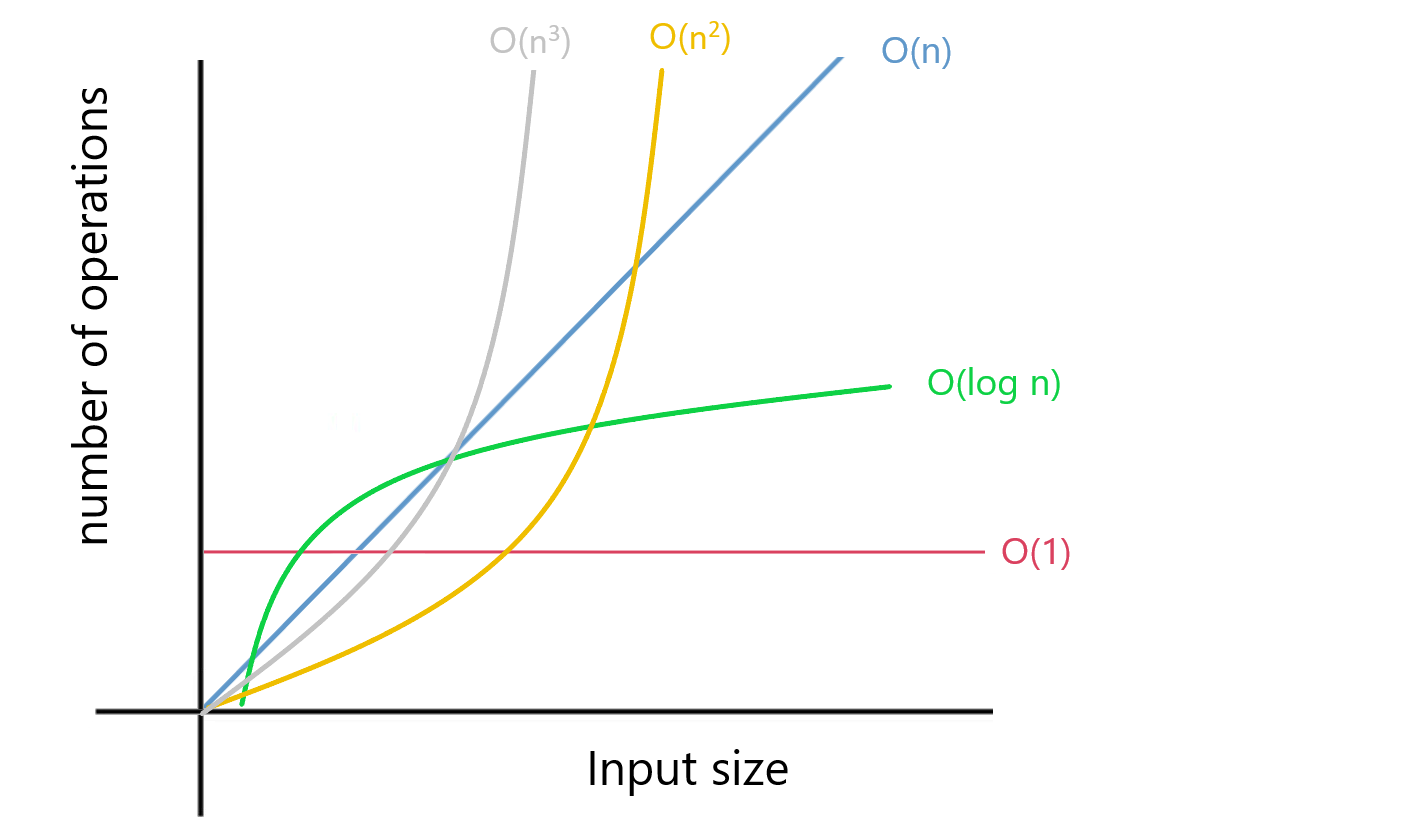
Mathematical expressions: $O(1)$, $O(n)$, $O(n^2)$...

Big O Notation

A graphical representation of different kinds of algorithms in Big O Notation.

$O(1)$

colors = ['green', 'yellow', 'blue', 'pink']

def constant(colors):
    print(colors[2])

constant(colors)

blue

$O(1)$

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple', 'red']

def constant(colors):
    print(colors[2])  # O(1)

constant(colors)

blue

$O(n)$

colors = ['green', 'yellow', 'blue', 'pink']

def linear(colors):
  for color in colors:
    print(color)    

linear(colors)

green

yellow

blue

pink

$O(n)$

colors = ['green', 'yellow', 'blue', 'pink'] # n=4

def linear(colors):
  for color in colors:
    print(color)    # O(4)

linear(colors)

n=4: 4 operations

$O(n)$

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple'] # n=7

def linear(colors):
  for color in colors:
    print(color)    # O(7)

linear(colors)

n=4: 4 operations
n=7: 7 operations
n=100: 100 operations
...
$O(n)$ complexity

$O(n^2)$

colors = ['green', 'yellow', 'blue']

def quadratic(colors):  
  for first in colors:
      for second in colors:
          print(first, second)

quadratic(colors)

n=3: (3 x 3) 9 operations
n=100: (100 x 100) 10,000 operations
quadratic pattern
$O(n^2)$ complexity

green green
green yellow
green blue
yellow green
yellow yellow
yellow blue
blue green
blue yellow
blue blue

$O(n^3)$

colors = ['green', 'yellow', 'blue']

def cubic(colors):  
  for color1 in colors:
      for color2 in colors:
          for color3 in colors:
              print(color1, color2, color3)

cubic(colors)

n=3: (3 x 3 x 3) 27 operations
n=10: (10 x 10 x 10) 1,000 operations
cubic pattern
$O(n^3)$ complexity

Calculating Big O Notation

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple']
other_colors = ['orange', 'brown']

def complex_algorithm(colors):
  color_count = 0

  for color in colors:
      print(color)
      color_count += 1

  for other_color in other_colors:
      print(other_color)
      color_count += 1

  print(color_count)

complex_algorithm(colors)

Calculating Big O Notation

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple']  # O(1)
other_colors = ['orange', 'brown']  # O(1)


def complex_algorithm(colors):
  color_count = 0          # O(1)


  for color in colors:
    print(color)           # O(n)
    color_count += 1       # O(n)


  for other_color in other_colors:
    print(other_color)     # O(m)
    color_count += 1       # O(m)


  print(color_count)       # O(1)


complex_algorithm(colors)  # O(4

Calculating Big O Notation

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple']  # O(1)
other_colors = ['orange', 'brown']  # O(1)

def complex_algorithm(colors):
  color_count = 0          # O(1)

  for color in colors:
    print(color)           # O(n)
    color_count += 1       # O(n)

  for other_color in other_colors:
    print(other_color)     # O(m)
    color_count += 1       # O(m)

  print(color_count)       # O(1)

complex_algorithm(colors)  # O(4 + 2n

Calculating Big O Notation

colors = ['green', 'yellow', 'blue', 'pink', 'black', 'white', 'purple']  # O(1)
other_colors = ['orange', 'brown']  # O(1)

def complex_algorithm(colors):
  color_count = 0          # O(1)

  for color in colors:
    print(color)           # O(n)
    color_count += 1       # O(n)

  for other_color in other_colors:
    print(other_color)     # O(m)
    color_count += 1       # O(m)

  print(color_count)       # O(1)

complex_algorithm(colors)  # O(4 + 2n + 2m)

Simplifying Big O Notation

Remove constants
- $O(4 + 2n + 2m)$ -> $O(n + m)$
Different variables for different inputs
- $O(n + m)$
Remove smaller terms
- $O(n + n^2)$

Simplifying Big O Notation

Remove constants
- $O(4 + 2n + 2m)$ -> $O(n + m)$
Different variables for different inputs
- $O(n + m)$
Remove smaller terms
- $O(n + n^2)$ -> $O(n^2)$

Let's practice!

Data Structures and Algorithms in Python