Resampling as a special type of Monte Carlo simulation

Monte Carlo Simulations in Python

Izzy Weber

Curriculum Manager, DataCamp

Resampling as a special type of Monte Carlo simulation

Monte Carlo simulations

Sample from probability distributions
Distributions either known or assumed
Rely on historical data or expertise to choose proper distributions

Resampling

Sample randomly from existing data
Existing data is implicit probability distribution
Assume that data is representative

Resampling methods

Sampling without replacement
- Used to draw a random sample
Sampling with replacement (or bootstrapping)
- Use to estimate the sampling distribution of almost any statistic
Permutation
- Often used to compare two groups

Sampling without replacement

Randomly draw two different states of the six states in New England

import random
def two_random_ne_states():

    ne_states=["Maine",
               "Vermont",
               "New Hampshire",
               "Massachusetts",
               "Connecticut",
               "Rhode Island"]

    return(random.sample(ne_states, 2))

two_random_ne_states()
two_random_ne_states()

['Massachusetts', 'Connecticut']
['New Hampshire', 'Maine']

Bootstrapping

Estimate the 95% confidence interval for the mean height of NBA players

import random
import numpy as np

nba_heights = [196, 191, 198, 216, 188, 185, 211, 201,
               188, 191, 201, 208, 191, 183, 196]
simu_heights = []

for i in range(1000):
    bootstrap_sample = random.choices(nba_heights, k=15)
    simu_heights.append(np.mean(bootstrap_sample))

upper = np.quantile(simu_heights, 0.975)
lower = np.quantile(simu_heights, 0.025)
print([np.mean(simu_heights), lower, upper])

[196.26666666666668, 191.8, 201.2]

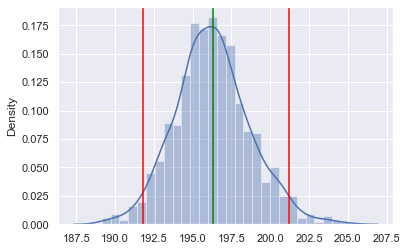
Visualization of bootstrap results

Plotting libraries:

seaborn
matplotlib

import seaborn as sns
import matplotlib.pyplot as plt

sns.displot(simu_heights)
plt.axvline(191.8, color="red")
plt.axvline(201.2, color="red")
plt.axvline(196.3, color="green")

a distribution plot of simulated heights

Permutation

Estimate 95% confidence interval of the mean difference between heights of NBA players and US males

us_heights = [165, 185, 179, 187, 193, 180, 178, 179, 171, 176, 
              169, 160, 140, 199, 176, 185, 175, 196, 190, 176]
nba_heights = [196, 191, 198, 216, 188, 185, 211, 201, 188, 191, 201, 208, 191, 183, 196]

all_heights = us_heights + nba_heights


simu_diff = []
for i in range(1000):
    perm_sample = np.random.permutation(all_heights)
    perm_nba, perm_adult = perm_sample[0:15], perm_sample[15:35]

    perm_diff = np.mean(perm_nba) - np.mean(perm_adult)
    simu_diff.append(perm_diff)

Permutation results

Difference in mean of NBA heights and adult American male heights:

np.mean(nba_heights) - np.mean(us_adult_height)

18.31666666666669

95% confidence interval for permutation of two random lists:

upper = np.quantile(simu_diff, 0.975)
lower = np.quantile(simu_diff, 0.025)
print([lower, upper])

[-10.033333333333331, 10.033333333333331]

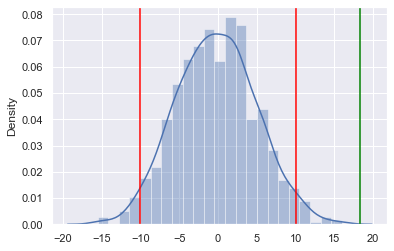
Visualizing permutation results

sns.distplot(simu_diff)
plt.axvline(-10.03, color="red")
plt.axvline(10.03, color="red")
plt.axvline(18.32, color="green")

a distribution plot of simulated heights

Let's practice!

Monte Carlo Simulations in Python