Sensitivity analysis

Monte Carlo Simulations in Python

Izzy Weber

Curriculum Manager, DataCamp

Sensitivity analysis

Helps us understand the impact of the range of inputs
Illustrates the patterns or trends when summarized in tables or plots

If we increase or decrease the values for bmi and hdl using a Monte Carlo simulation, how will the predicted y values (disease progression) change?

Defining the parameters

cov_dia = dia[["age", "bmi", "bp", "tc", "ldl", "hdl", "tch", "ltg", "glu"]].cov()
mean_dia = dia[["age", "bmi", "bp", "tc", "ldl", "hdl", "tch", "ltg", "glu"]].mean()

Defining the simulation function

def simulate_bmi_hdl(cov_dia, mean_list):

    list_ys = []
    for i in range(50):
        simulation_results = st.multivariate_normal.rvs(mean=mean_list, 
                                                        size=500, cov=cov_dia)
        df_results = pd.DataFrame(simulation_results, 
                                  columns=["age","bmi","bp","tc","ldl","hdl","tch","ltg","glu"])
        predicted_y = regr_model.predict(df_results)
        df_y = pd.DataFrame(predicted_y, columns=["predicted_y"])
        df_summary = pd.concat([df_results, df_y], axis=1)
        y = np.mean(df_summary["predicted_y"]) 
        list_ys.append(y)

    return(np.mean(list_ys))

Perform simulations with a range of input parameters

hdl = []
bmi = []
simu_y = []
for mean_hdl_inc in np.arange(-20, 50, 30): 
    for mean_bmi_inc in np.arange(-7, 11, 3):

        mean_list = mean_dia + np.array([0, mean_bmi_inc, 0, 0, 0, mean_hdl_inc, 0, 0, 0])
        hdl.append(mean_hdl_inc)
        bmi.append(mean_bmi_inc)

        mean_y = simulate_bmi_hdl(cov_dia, mean_list)

        simu_y.append(mean_y)

df_sa = pd.concat([pd.Series(hdl), pd.Series(bmi), pd.Series(simu_y)], axis=1)

df_sa.columns = ["hdl_inc", "bmi_inc", "y"]

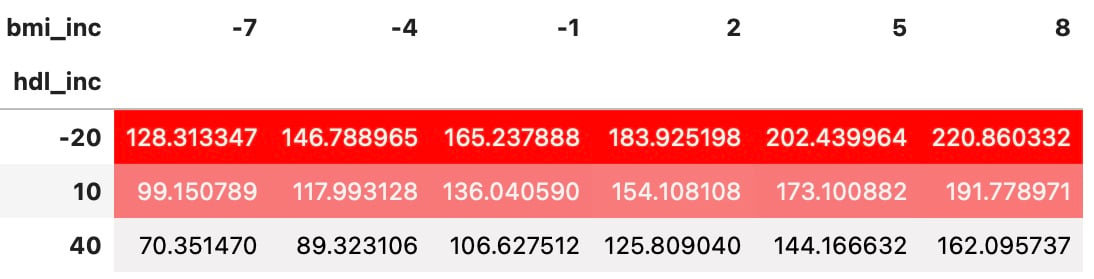
Styled DataFrames of sensitivity analysis results

df_sa.sort_values(by=['hdl_inc', 'bmi_inc']).pivot(index='hdl_inc',
                                             columns='bmi_inc',
                                             values='y').style.background_gradient(
                                             cmap=sns.light_palette("red", as_cmap=True))

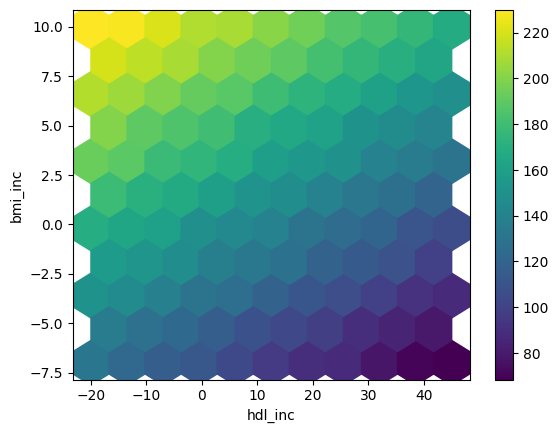
The df_sa after sorting, pivoting, and styling

Hexbin plot for sensitivity analysis results

df_sa.plot.hexbin(x='hdl_inc',y='bmi_inc', C='y',
                    reduce_C_function=np.mean,
                    gridsize=10, cmap="viridis",
                    sharex=False)

A hexbin of df_sa

Hexbin plot for dense parameter space

Let's practice!

Monte Carlo Simulations in Python