The Importance of Dimensionality Reduction in Data and Model Building
Dimensionality Reduction in R

Matt Pickard
Owner, Pickard Predictives, LLC
The curse of dimensionality
- a marginal increase in dimensionality requires an exponential increase in data volume
- data sparsity → bias and overfitting

The curse of dimensionality
- problems dealing with high-dimensional data
- a marginal increase in dimensionality requires an exponential increase in data volume
- data sparsity → bias and overfitting

The curse of dimensionality
The curse of dimensionality

Sparsity
Sparsity
Sparsity
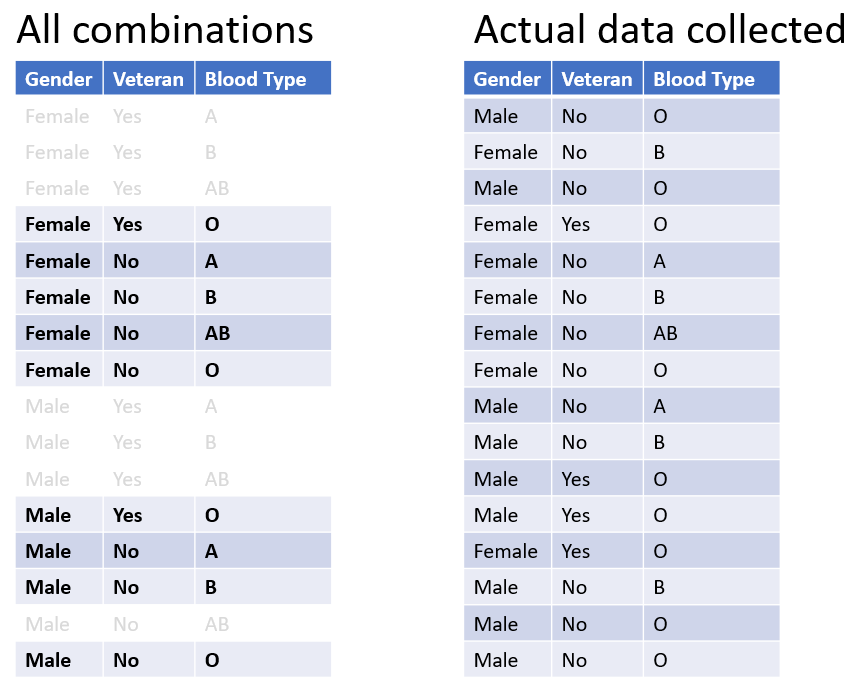
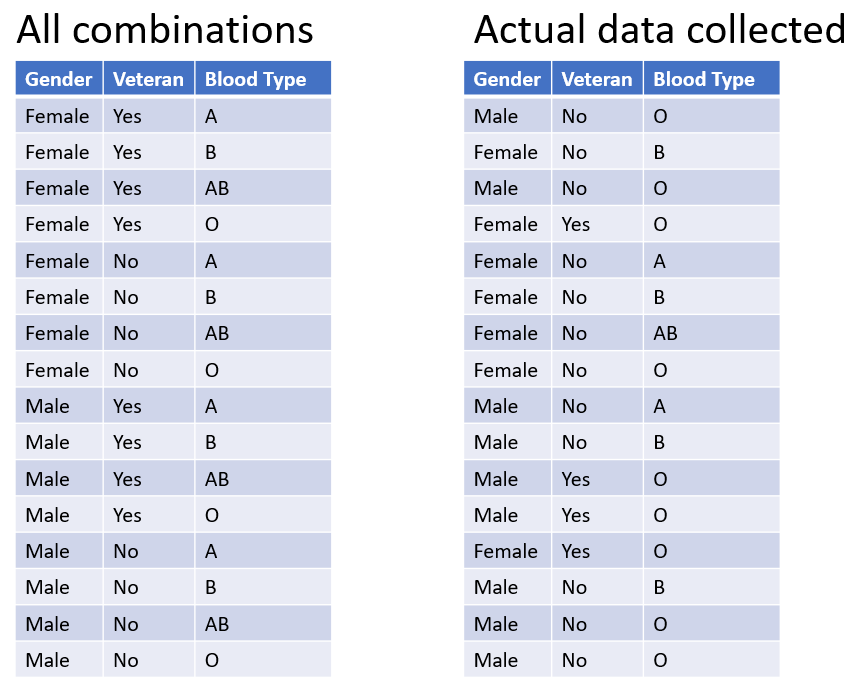
Sparsity: training and test sets

Sparsity: training and test sets
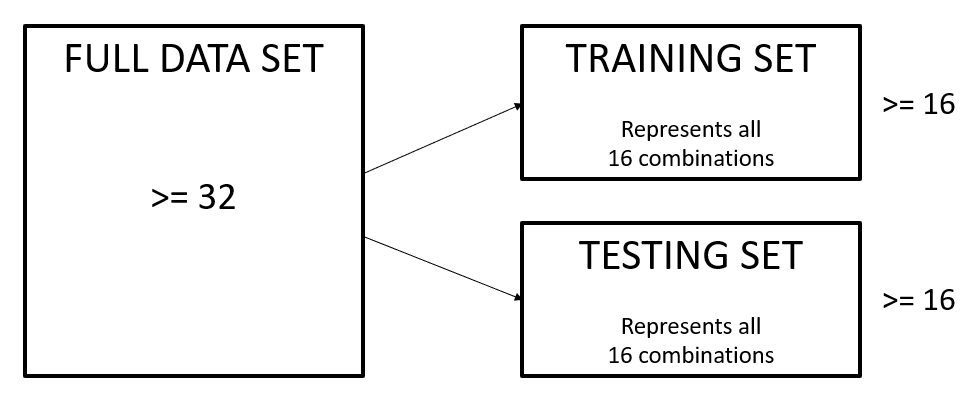
Sparsity: training and test sets

Sparsity: training and test sets
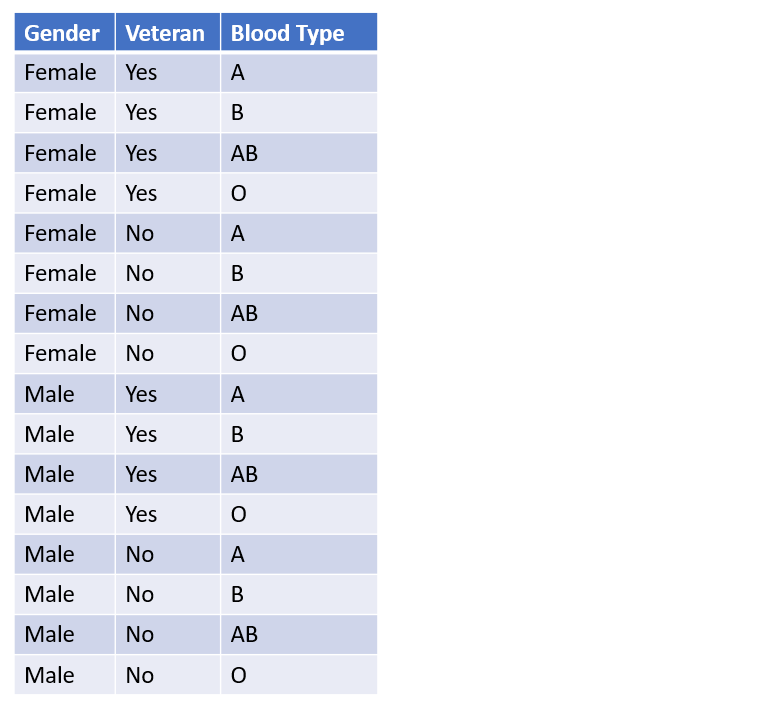
Calculate minimum number of observations
blood_type_df <-
expand_grid(
gender = c("Female", "Male"),
veteran = c("Yes", "No"),
bloodtype = c("A", "B", "AB", "O")
)
# A tibble: 16 × 3
gender veteran bloodtype
<chr> <chr> <chr>
1 Female Yes A
2 Female Yes B
3 Female Yes AB
4 Female Yes O
5 Female No A
6 Female No B
7 Female No AB
8 Female No O
9 Male Yes A
... ... ...
Calculate minimum number of observations
blood_type_df %>% summarize(across(everything(), ~ length(unique(.)))) %>%prod()
16
NOTE: That's the number to represent each combination only once!
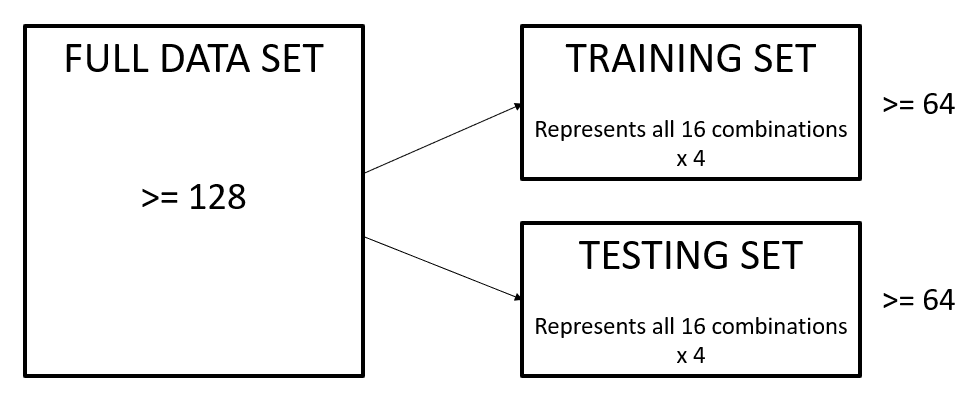
Multiple representations of each combination
blood_type_df %>%
summarize(across(everything(), ~ length(unique(.))) %>%
prod() * 4
128
Let's practice!
Dimensionality Reduction in R

