Information and feature importance
Dimensionality Reduction in R

Matt Pickard
Owner, Pickard Predictives, LLC

1 Provost, Foster; Fawcett, Tom (2013-07-27). Data Science for Business: What you need to know about data mining and data-analytic thinking. O'Reilly Media. Kindle Edition.
Feature importance
Feature importance: a measure of information in model building
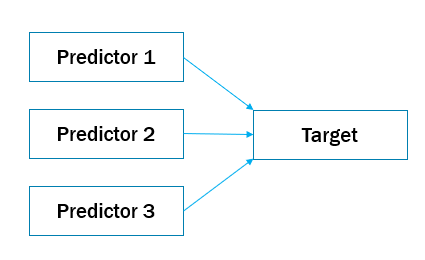
Many ways to measure feature importance
- Correlation (with target variable)
- Standardize regression coefficients
- Information gain
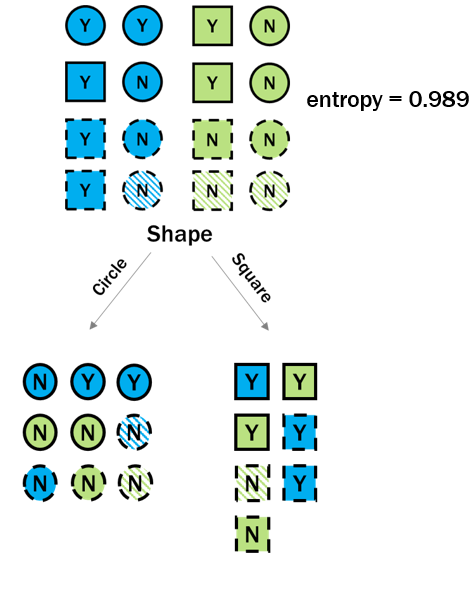
Decision tree example
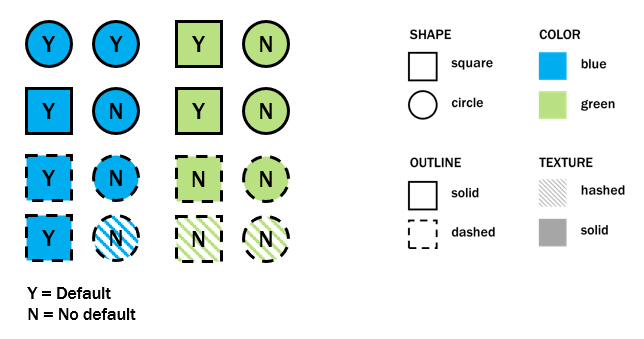
Decision tree and information gain
Information gain - the amount of information we know about one variable by observing another variable
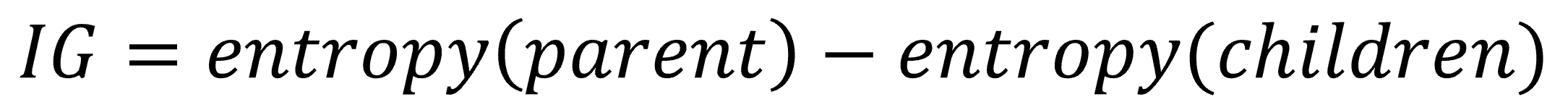
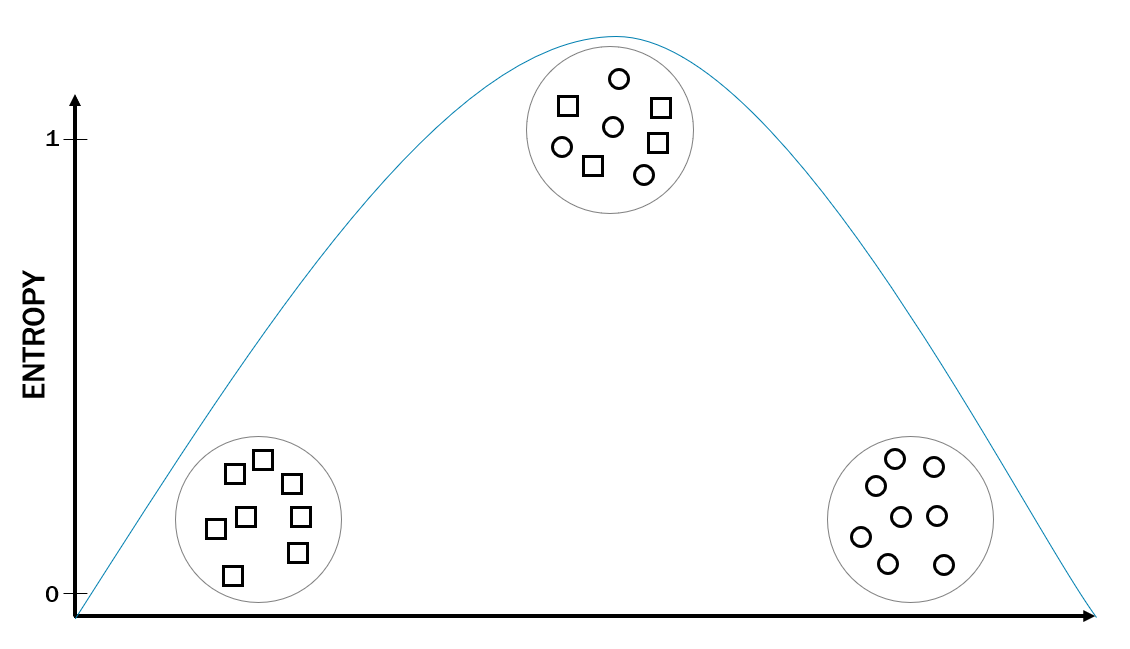
Entropy
- A measure of disorder
- As purity goes up, entropy goes down
- Entropy values range from 0 (perfect purity) to 1 (perfect entropy)
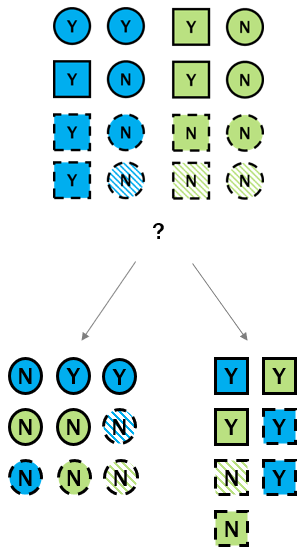
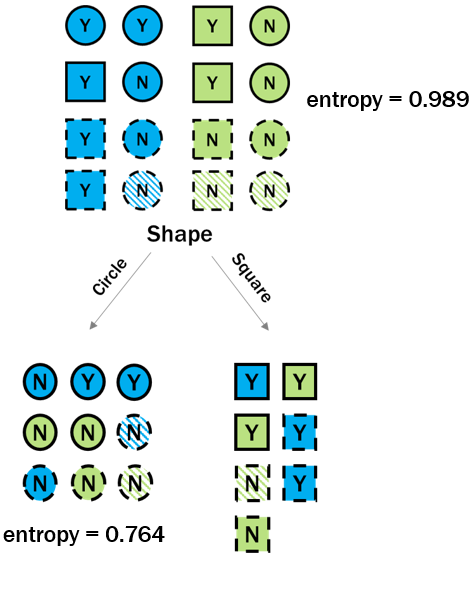
Entropy: root node
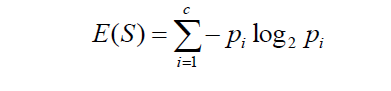
p_yes <- 7/16p_no <- 9/16entropy_root <- -(p_yes * log2(p_yes)) + -(p_no * log2(p_no))entropy_root
0.989
Entropy: children nodes
p_left_yes <- 2/9p_left_no <- 7/9entropy_left <- -(p_left_yes * log2(p_left_yes)) + -(p_left_no * log2(p_left_no))
Entropy: children nodes
p_left_yes <- 2/9p_left_no <- 7/9entropy_left <- -(p_left_yes * log2(p_left_yes)) + -(p_left_no * log2(p_left_no))entropy_left
0.764
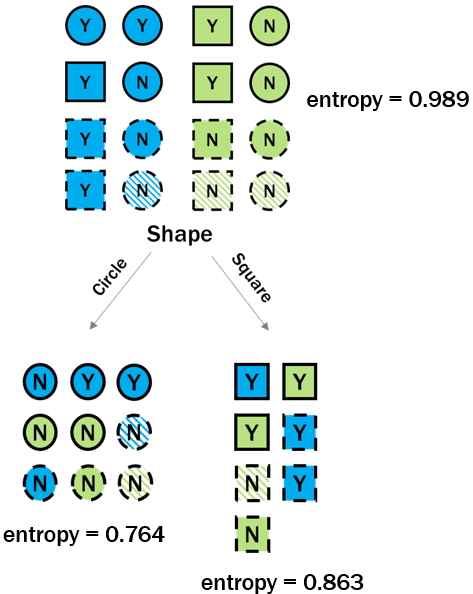
Entropy: children nodes
p_right_yes <- 5/7p_right_no <- 2/7entropy_right <- -(p_right_yes * log2(p_right_yes)) + -(p_right_no * log2(p_right_no))

Entropy: children nodes
p_right_yes <- 5/7p_right_no <- 2/7entropy_right <- -(p_right_yes * log2(p_right_yes)) + -(p_right_no * log2(p_right_no))entropy_right
0.863
Information gain: root to children
p_left <- 9/16p_right <- 7/16info_gain <- entropy_root - (p_left * entropy_left + p_right * entropy_right)info_gain
0.181

Compare information gain across features
| Feature | Information Gain |
|---|---|
| shape | 0.181 |
| texture | 0.180 |
| outline | 0.106 |
| color | 0.106 |

Let's practice!
Dimensionality Reduction in R

