Non-parametric tests
Foundations of Inference in Python

Paul Savala
Assistant Professor of Mathematics
Non-parametric tests
- May have assumptions
- Don't require normality
- Applies to a broad range of data
- Sometimes less powerful
- Useful for ranked order (e.g. star rankings)
Parametric tests
- Independent sample t-test
- ANOVA
- Paired sample t-test
- Pearson's R
Non-parametric
- Wilcoxon-Mann-Whitney U test
- Kruskal-Wallis test
- Mood's median test
- Kendall's tau
Mood's median test
Compares medians from two paired measurements
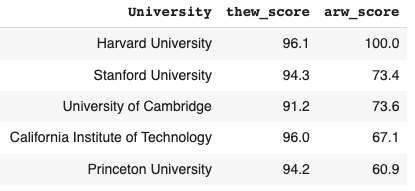
Likely not normally distributed
s, p_value, m, table = stats.median_test(df['thew_score'], df['arw_score'])
Mood's median test
print(p_value < 0.05)
TRUE
- Conclusion: Different median rankings
- t-tests assume normality (Mood's median test does not)
- Valid inference only when data and assumptions match
- Use the right tool for the job!
Kendall's tau
- Values between -1 and 1
- $\tau = -1$: Complete disagreement
- $\tau = 0$: No correlation
- $\tau = 1$: Complete agreement
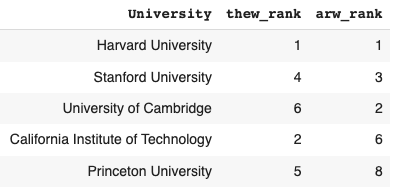
tau, p_value = stats.kendalltau( df['thew_rank'], df['arw_rank'])print(tau, p_value < 0.05)
0.651, TRUE
Let's practice!
Foundations of Inference in Python

