Effect size

Foundations of Inference in Python

Paul Savala

Assistant Professor of Mathematics

What is effect size?

A doctor holding a broken cigarette.

Effect size: Measure of strength between two variables

A collection of junk food.

Why measure effect size

Measures strength of relationship
Smoking: Large effect size
Poor diet: Small effect size

P-Values

Does a relationship exist?
Comes from hypothesis test

Effect size

How strong is the relationship?
Separate from a hypothesis test

Effect size for means - Cohen's d

$n_1 = \text{Sample size of group one}$

$n_2 = \text{Sample size of group two}$

$s_1 = \text{Standard deviation of group one}$

$s_2 = \text{Standard deviation of group two}$

$\overline{x}_1 = \text{Mean of group one}$

$\overline{x}_2 = \text{Mean of group two}$

$s = \displaystyle\sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}}$

Cohen's $d = \displaystyle\frac{\overline{x}_1 - \overline{x}_2}{s}$

Interpreting Cohen's d

0.01 - Very small
0.20 - Small
0.50 - Medium
0.80 - Large
1.20 - Very large

Cohen's $d = 0.6$

Medium-to-large effect size

¹ https://books.google.com/books?id=2v9zDAsLvA0C&pg=PP1 https://doi.org/10.22237%2Fjmasm%2F1257035100

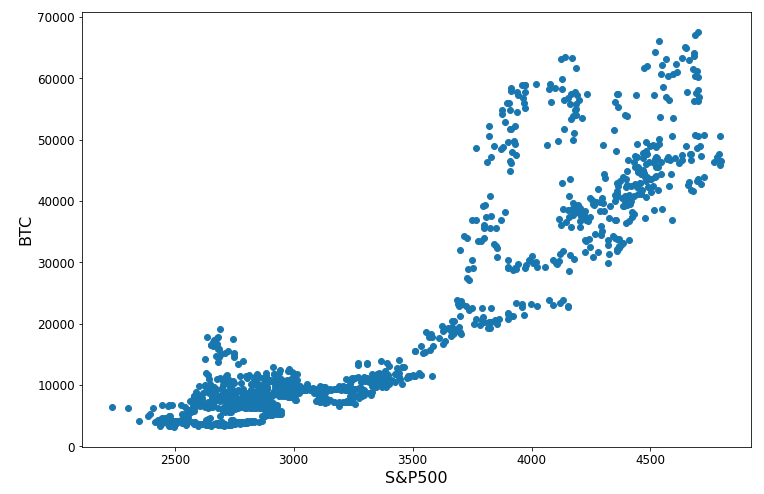
Effect size for correlation

r, p_value = stats.pearsonr(
    btc_sp_df['Close_BTC'], 
    btc_sp_df['Close_SP500']
    )


print(r**2)

0.82

$R^2:$ Percent of variation in one variable explained by knowing the other

A scatter plot with the S and P 500 closing price on the x axis and the Bitcoin closing price on the y-axis. The graph is roughly linear with a positive slope.

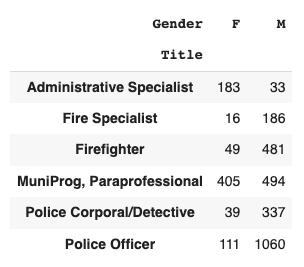
Effect size for categorical variables

$\chi^2$ = Chi-squared statistic from contingency table
$n$ = total number of data points
$d$ = degrees of freedom = $min(\text{rows}-1, \text{cols}-1)$

Cramer's $V = \displaystyle\sqrt{\frac{\chi^2/n}{d}}$

Calculating Cramer's V

chi2, p, d, e = stats.chi2_contingency(
    contingency_table)


dof = min(6-1, 2-1) = 1
n = 3394


v = np.sqrt((chi2 / n) / dof)

v = 0.52

A table showing male and females along with job titles. The table shows how many males and females hold each job title.

¹ https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)

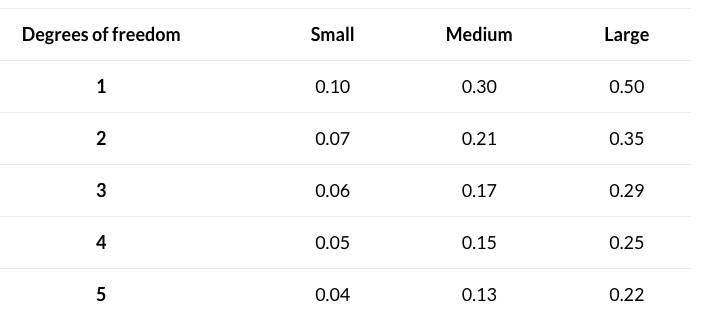
Interpreting Cramer's V

Cramer's V = 0.52, Degrees of Freedom = 1

A table showing degrees of freedom as one through five, and the Cramer's V values needed for an effect size of small, medium and large. Small goes 0.1, 0.07, 0.06, 0.05, 0.04. Medium goes 0.3, 0.21, 0.17, 0.15, 0.13. Large goes 0.5, 0.35, 0.29, 0.25, 0.22.

¹ https://www.statology.org/interpret-cramers-v

Let's practice!

Foundations of Inference in Python