Transformations for variance stabilization
Forecasting in R

Rob J. Hyndman
Professor of Statistics at Monash University
Variance stabilization
If the data show increasing variation as the level of the series increases, then a transformation can be useful
$y_1,...,y_n$: original observations, $w_1,...,w_n$: transformed observations
| Square root | $w_t = \sqrt{y_t}$ | $\downarrow$ |
| Cube root | $w_t = \sqrt[3]{y_t}$ | Increasing |
| Logarithm | $w_t = \text{log}(y_t)$ | Strength |
| Inverse | $w_t = -1/y_t$ | $\downarrow$ |
Variance stabilization
autoplot(usmelec) +
xlab("Year") + ylab("") +
ggtitle("US monthly net electricity generation")
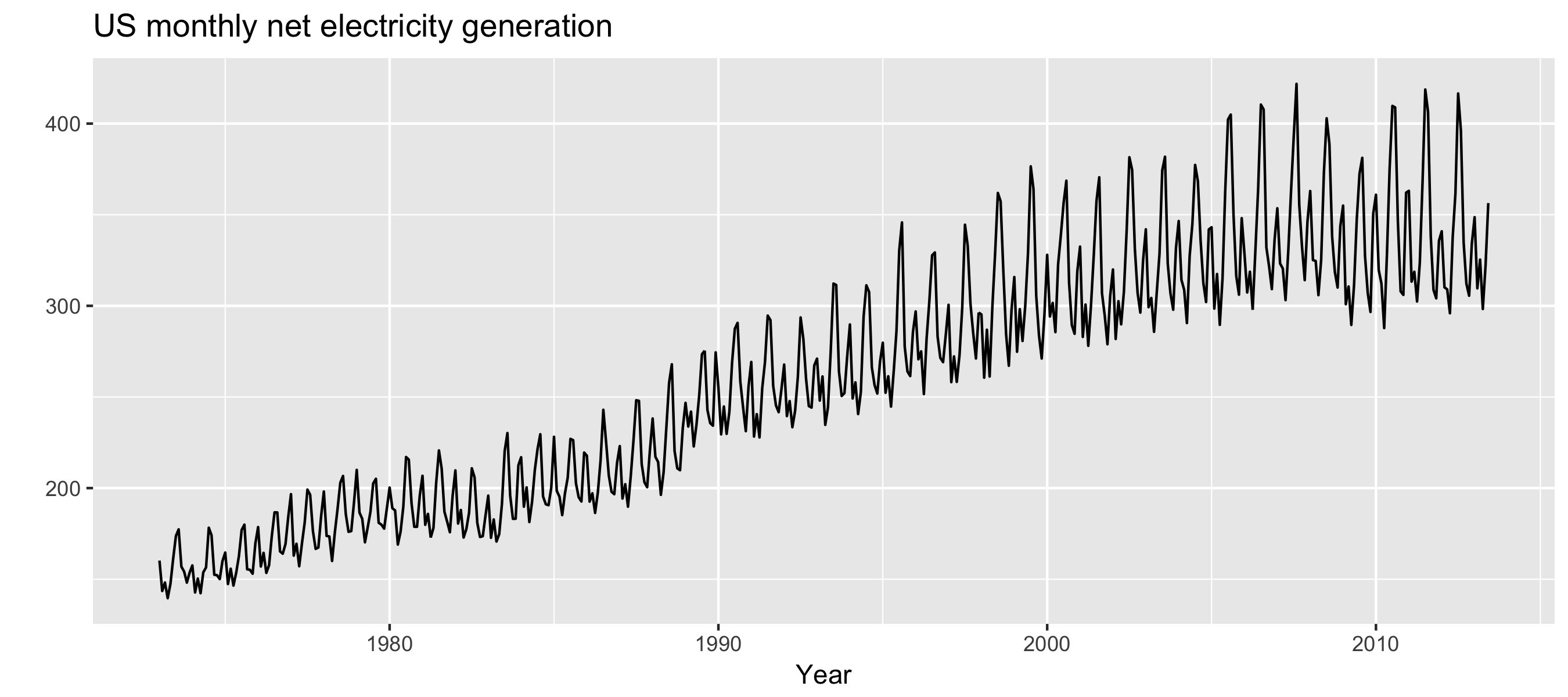
Variance stabilization
autoplot(usmelec^0.5) +
xlab("Year") + ylab("") +
ggtitle("Square root electricity generation")
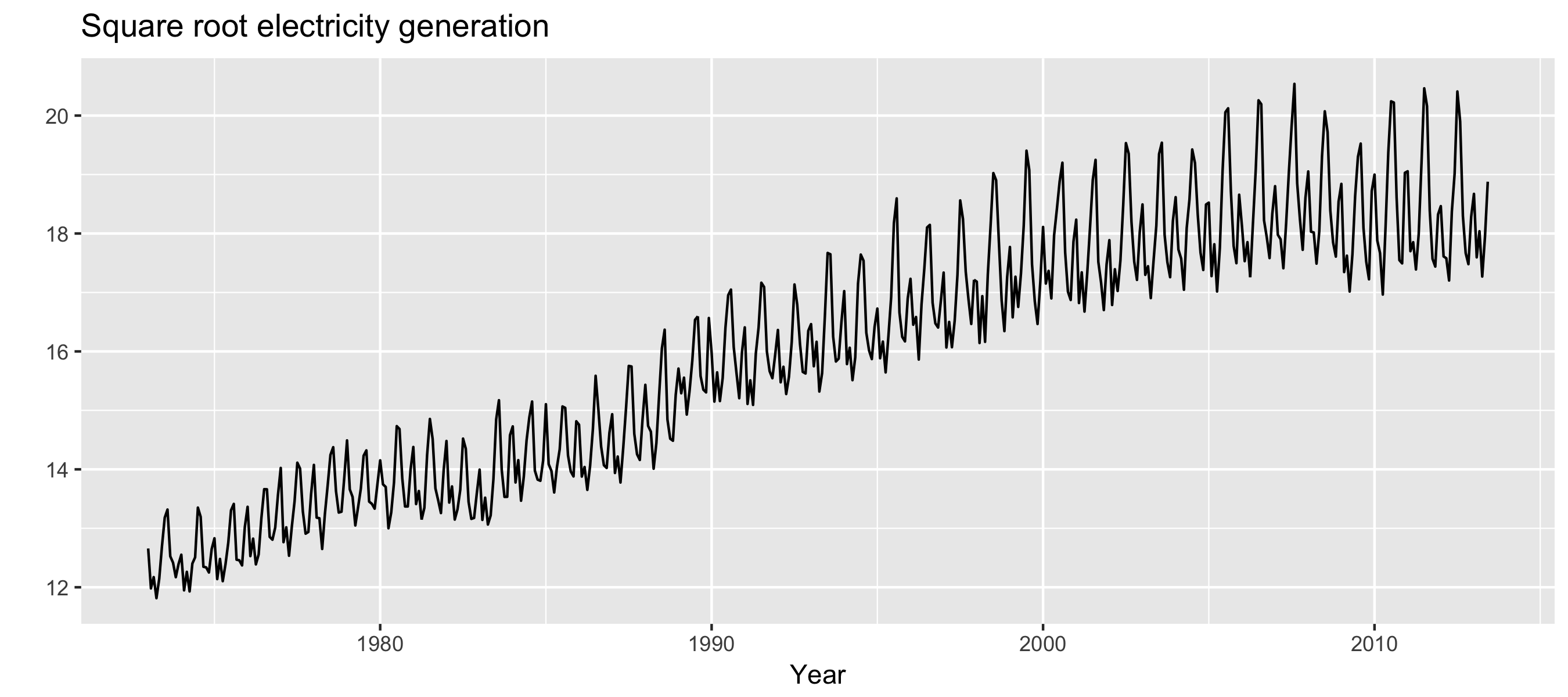
Variance stabilization
autoplot(usmelec^0.33333) +
xlab("Year") + ylab("") +
ggtitle("Cube root electricity generation")
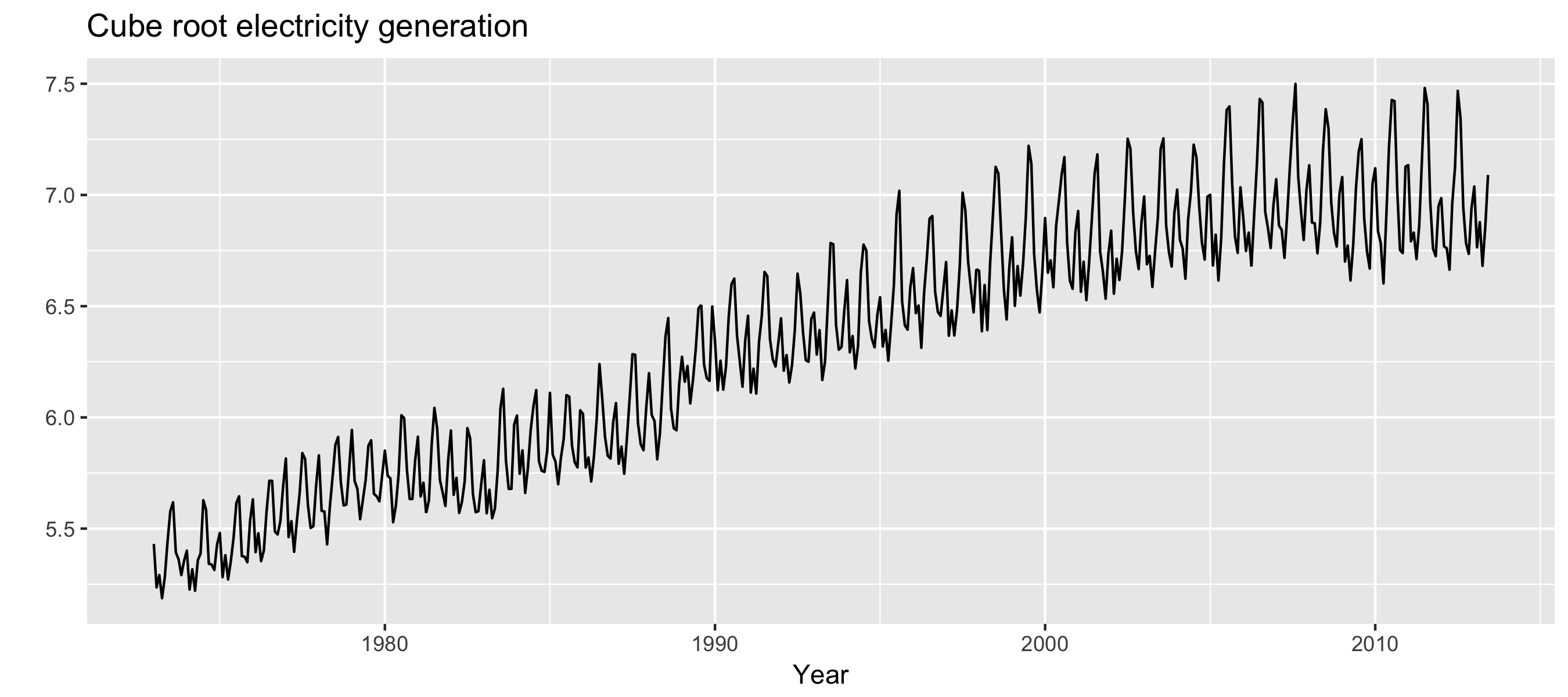
Variance stabilization
autoplot(log(usmelec)) +
xlab("Year") + ylab("") +
ggtitle("Log electricity generation")
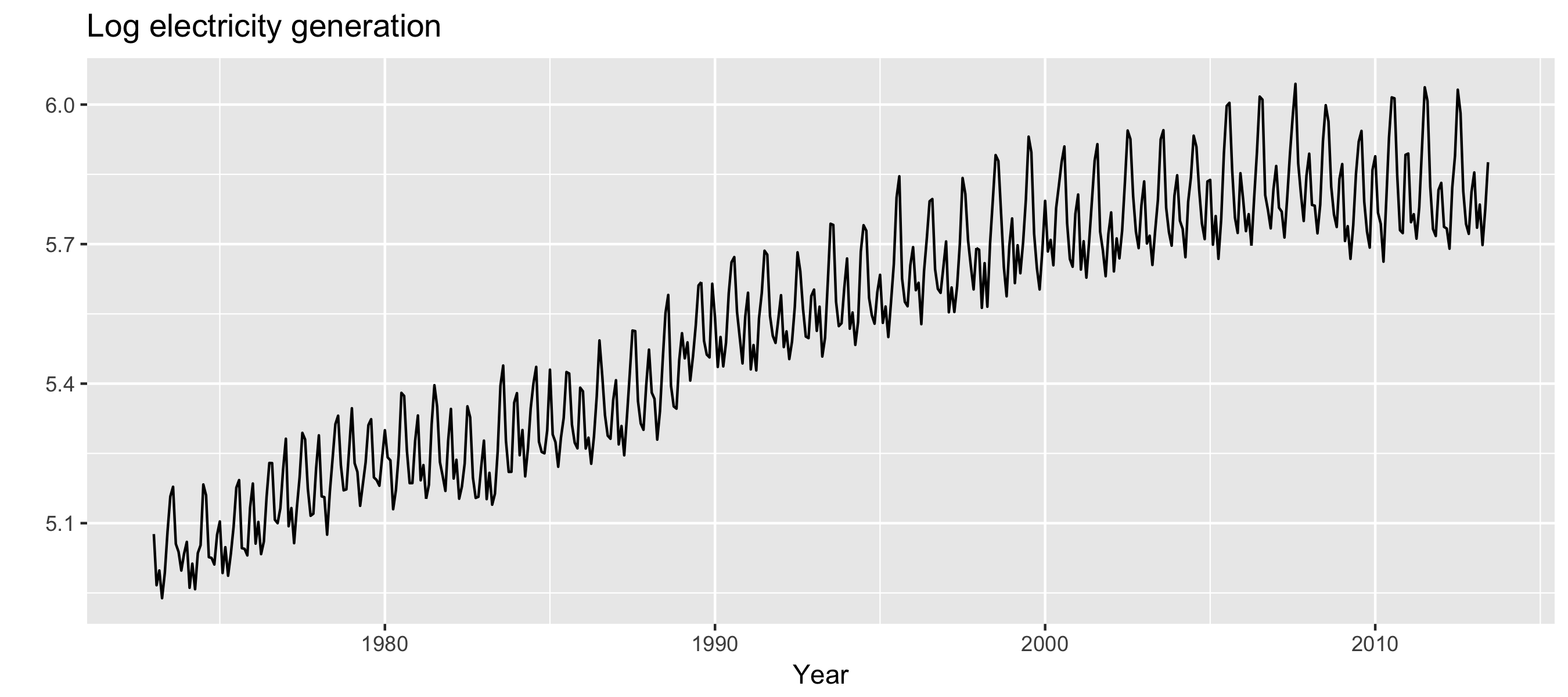
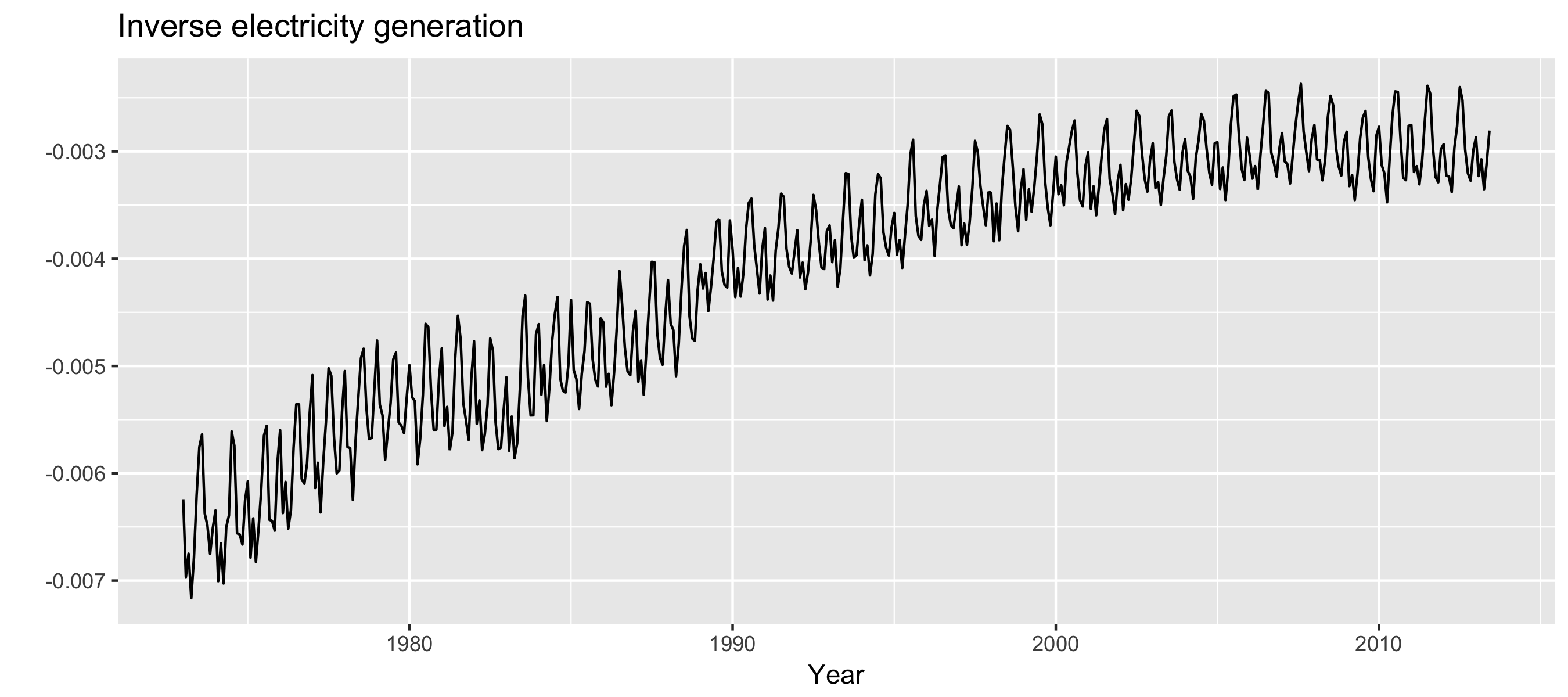
Variance stabilization
autoplot(-1/usmelec) +
xlab("Year") + ylab("") +
ggtitle("Inverse electricity generation")
Box-Cox transformations
- Each of these transformations is close to a member of the family of Box-Cox transformations
$$w_t = \begin{cases} log(y_t) & \lambda = 0 \\ (y_t^\lambda - 1)/\lambda & \lambda \neq 0 \end{cases}$$
- $\lambda = 1 \ $: No substantive transformation
- $\lambda = \frac{1}{2} \ $: Square root plus linear transformation
- $\lambda = \frac{1}{3} \ $: Cube root plus linear transformation
- $\lambda = 0 \ $: Natural logarithm transformation
- $\lambda = -1 \ $: Inverse transformation
Box-Cox transformations
BoxCox.lambda(usmelec)
-0.5738331
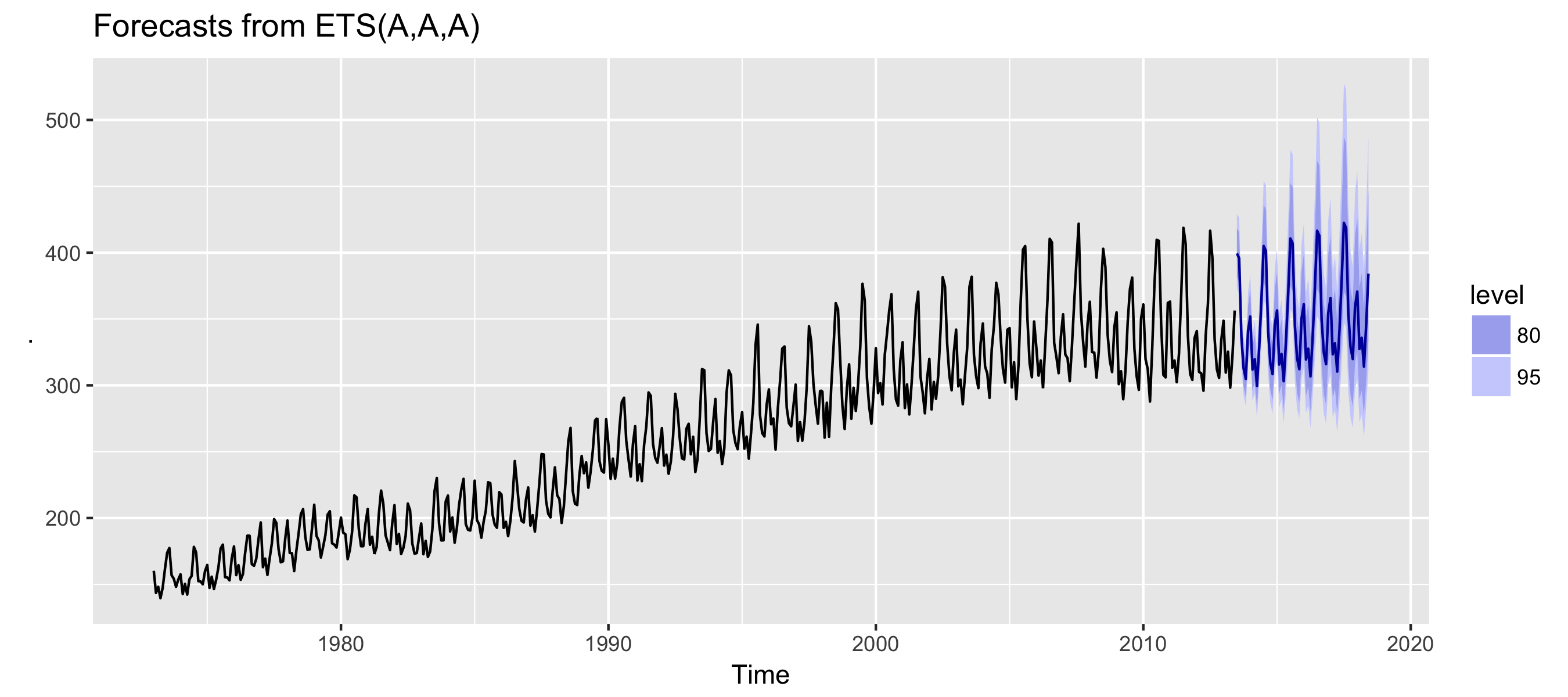
Back-transformation
usmelec %>%
ets(lambda = -0.57) %>%
forecast(h = 60) %>%
autoplot()
Let's practice!
Forecasting in R

