Dynamic regression
Forecasting in R

Rob J. Hyndman
Professor of Statistics at Monash University
Dynamic regression
Regression model with ARIMA errors:
$y_t = \beta_0 + \beta_1 x_{1,t} + ... + \beta_r x_{r,t} + e_t$
- $y_t$ modeled as function of r explanatory variables $\ x_{1,t},...,x_{r,t}$
Dynamic regression
Regression model with ARIMA errors:
$y_t = \beta_0 + \beta_1 x_{1,t} + ... + \beta_r x_{r,t} + e_t \leftarrow$
- $y_t$ modeled as function of r explanatory variables $\ x_{1,t},...,x_{r,t}$
- In dynamic regression, we allow $e_t$ to be an ARIMA process
Dynamic regression
Regression model with ARIMA errors:
$y_t = \beta_0 + \beta_1 x_{1,t} + ... + \beta_r x_{r,t} + e_t$
- $y_t$ modeled as function of r explanatory variables $\ x_{1,t},...,x_{r,t}$
- In dynamic regression, we allow $e_t$ to be an ARIMA process
- In ordinary regression, we assume that $e_t$ is white noise
US personal consumption and income
autoplot(uschange[,1:2], facets = TRUE) +
xlab("Year") + ylab("") +
ggtitle("Quarterly changes in US consumption
and personal income")
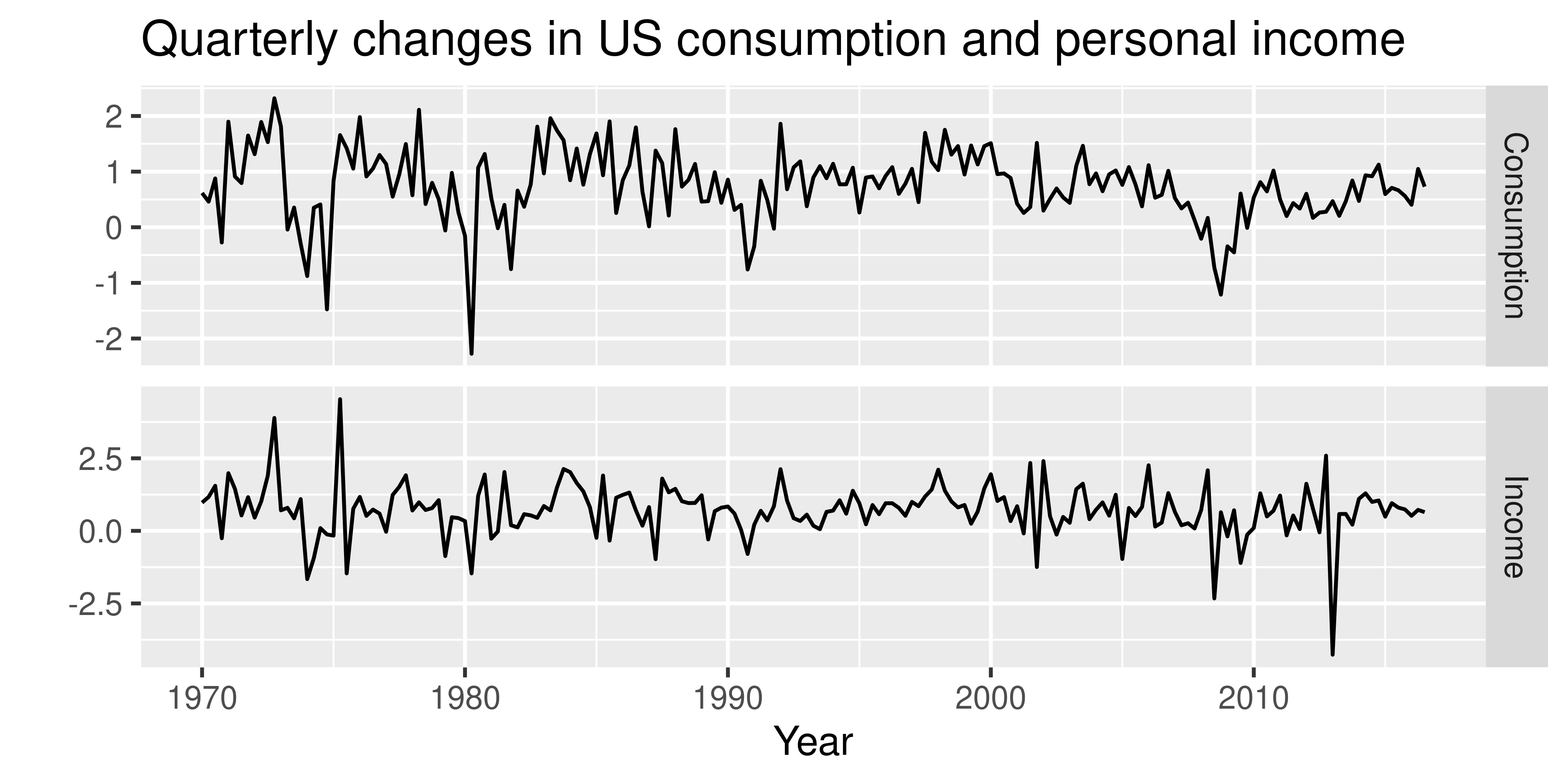
US personal consumption and income
ggplot(aes(x = Income, y = Consumption),
data = as.data.frame(uschange)) +
geom_point() +
ggtitle("Quarterly changes in US consumption and
personal income")
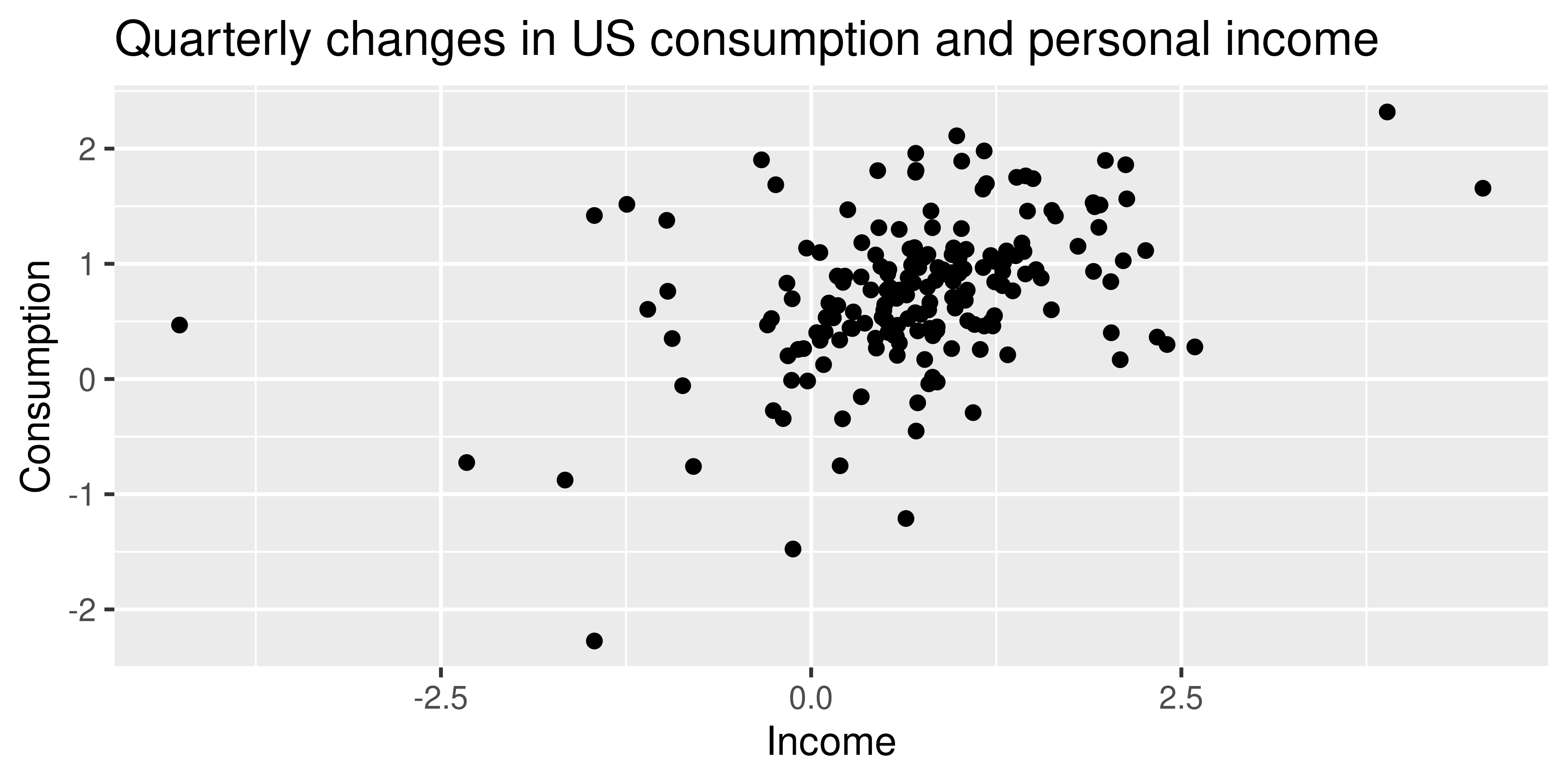
Dynamic regression model for US personal consumption
fit <- auto.arima(uschange[,"Consumption"],
xreg = uschange[,"Income"])
fit
Series: uschange[, "Consumption"]
Regression with ARIMA(1,0,2) errors
Coefficients:
ar1 ma1 ma2 intercept xreg
0.6922 -0.5758 0.1984 0.5990 0.2028
s.e. 0.1159 0.1301 0.0756 0.0884 0.0461
sigma^2 = 0.3219: log likelihood = -156.95
AIC=325.91 AICc=326.37 BIC=345.29
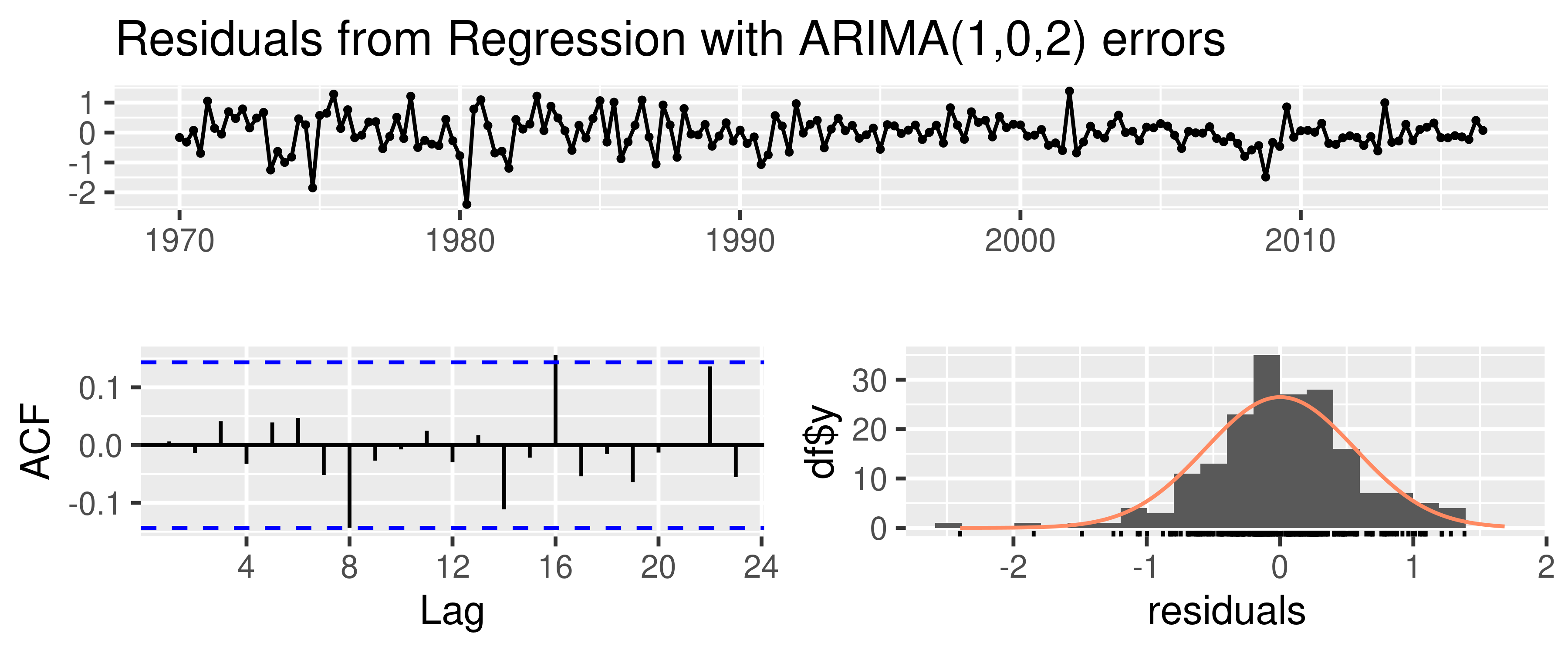
Residuals from dynamic regression model
checkresiduals(fit)
Ljung-Box test
data: Residuals from Regression with ARIMA(1,0,2) errors
Q* = 5.8916, df = 5, p-value = 0.3169
Model df: 3. Total lags used: 8
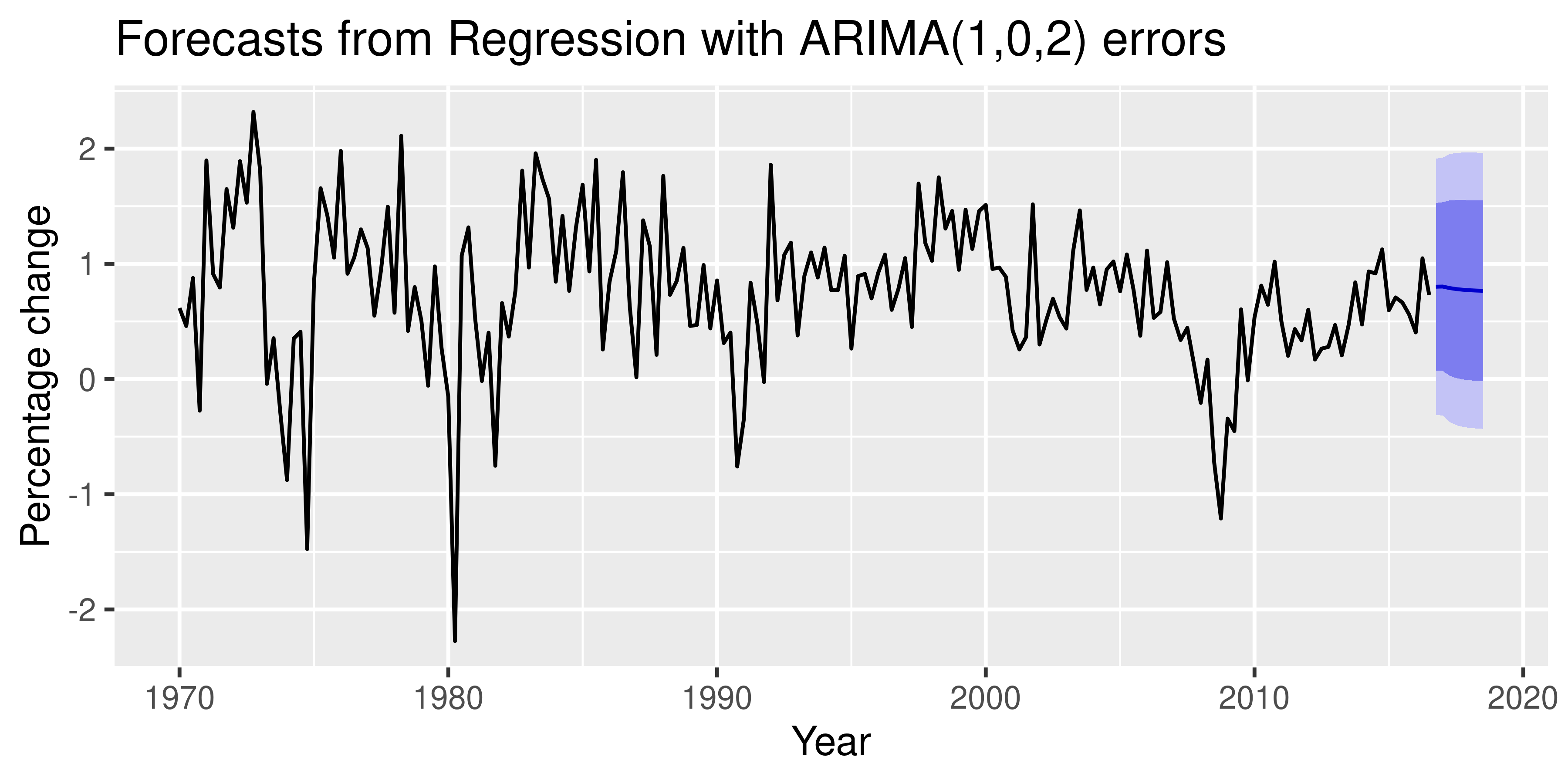
Forecasts from dynamic regression model
fcast <- forecast(fit, xreg = rep(0.8, 8))
autoplot(fcast) +
xlab("Year") + ylab("Percentage change")
Let's practice!
Forecasting in R

