Exponentially weighted forecasts

Forecasting in R

Rob J. Hyndman

Professor of Statistics at Monash University

Simple exponential smoothing

Forecasting Notation: $\hat y_{t + h \vert t} = \text{ point forecast of } \ \hat y_{t + h} \ \text{given data }\ y_1,...,y_t$

Forecast Equation: $\hat y_{t + h \vert t} = \alpha y_t + \alpha (1-\alpha ) y_{t-1} + \alpha (1-\alpha )^2 y_{t-2} +...$

$$where \ 0 \leq \alpha \leq 1 $$

Forecasting in R

Simple exponential smoothing

Observation $\alpha$ = 0.2 $\alpha$ = 0.4 $\alpha$ = 0.6 $\alpha$ = 0.8
$y_t$ 0.2 0.4 0.6 0.8
$y_{t-1}$ 0.16 0.24 0.24 0.16
$y_{t-2}$ 0.128 0.144 0.096 0.032
$y_{t-3}$ 0.1024 0.0864 0.0384 0.0064
$y_{t-4}$ (0.2)(0.8)$^4$ (0.4)(0.6)$^4$ (0.6)(0.4)$^4$ (0.8)(0.2)$^4$
$y_{t-5}$ (0.2)(0.8)$^5$ (0.4)(0.6)$^5$ (0.6)(0.4)$^5$ (0.8)(0.2)$^5$
Forecasting in R

Simple exponential smoothing

 

Component form
Forecast equation $\hat{y}_{t+h \mid t} = \ell_t$
Smoothing equation $\ell_t = \alpha y_t + (1-\alpha)\ell_{t-1}$

 

  • $\ell_t \ $ is the level (or the smoothed value) of the series at time $t$
  • We choose $\alpha$ and $\ell_0$ by minimizing SSE:

$$SSE = \sum_{t=1}^T (y_t - \hat y_{t\vert t-1})^2$$

Forecasting in R

Example: oil production

oildata <- window(oil, start = 1996)    # Oil Data
fc <- ses(oildata, h = 5)               # Simple Exponential Smoothing
summary(fc)

Forecast method: Simple exponential smoothing
Model Information:
Simple exponential smoothing
Call:
 ses(y = oildata, h = 5)
  Smoothing parameters:
    alpha = 0.8339
  Initial states:
    l = 446.5759
  sigma:  28.12
*** Truncated due to space
Forecasting in R

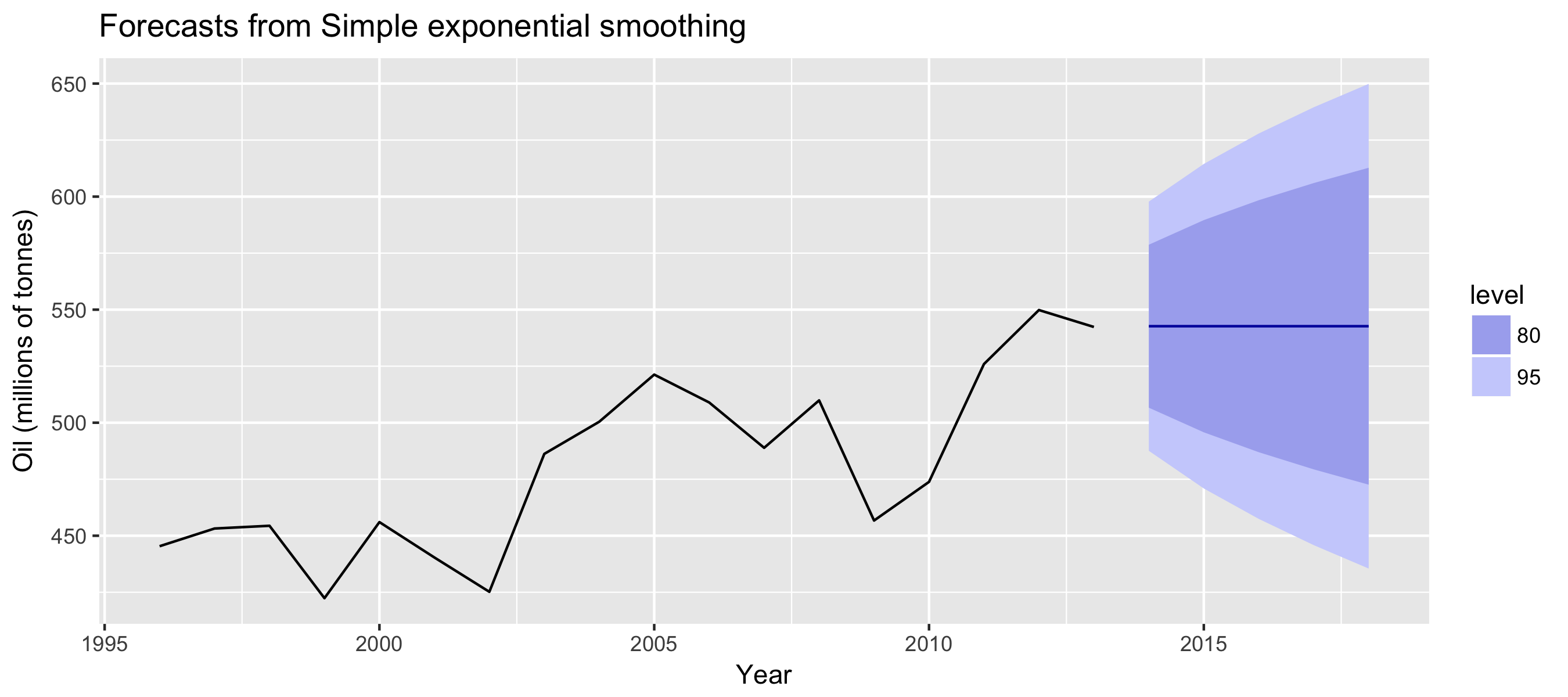
Example: oil production

autoplot(fc) +
  ylab("Oil (millions of tonnes)") + xlab("Year")

ch3_vid1_oil_simp_exp.png

Forecasting in R

Let's practice!

Forecasting in R

Preparing Video For Download...