Exponential smoothing methods with trend and seasonality

Forecasting in R

Rob J. Hyndman

Professor of Statistics at Monash University

Holt-Winters' additive method

Holt-Winters additive method
$\hat{y}_{t+h \mid t} = \ell_t + hb_t + s_{t-m+h_m^+}$
$\ell_t = \alpha(y_t - s_{t-m} )+ (1-\alpha)(\ell_{t-1} + b_{t-1})$
$b_t = \beta^*(\ell_t = \ell_{t-1}) + (1 - \beta^*) b_{t-1}$
$s_t = \gamma(y_t - \ell_{t-1} - b_{t-1}) + (1 - \gamma)s_{t-m}$

  • $s_{t-m+h_m^+}$ = seasonal component from final year of data

  • Smoothing parameters: $0 \leq \alpha \leq 1, \ 0 \leq \beta^* \leq 1, \ 0 \leq \gamma \leq 1 - \alpha$

  • $m$ = period of seasonality (e.g. $m = 4$ for quarterly data)

  • Seasonal component averages zero

Forecasting in R

Holt-Winters' multiplicative method

Holt-Winters multiplicative method
$\hat{y}_{t+h \mid t} = (\ell_t + hb_t)s_{t-m+h_m^+}$
$\ell_t = \alpha(\frac{y_t}{s_{t-m}} )+ (1-\alpha)(\ell_{t-1} + b_{t-1})$
$b_t = \beta^*(\ell_t = \ell_{t-1}) + (1 - \beta^*) b_{t-1}$
$s_t = \gamma\frac{y_t}{\ell_{t-1} - b_{t-1}} + (1 - \gamma)s_{t-m}$

 

  • Seasonal component averages one
Forecasting in R

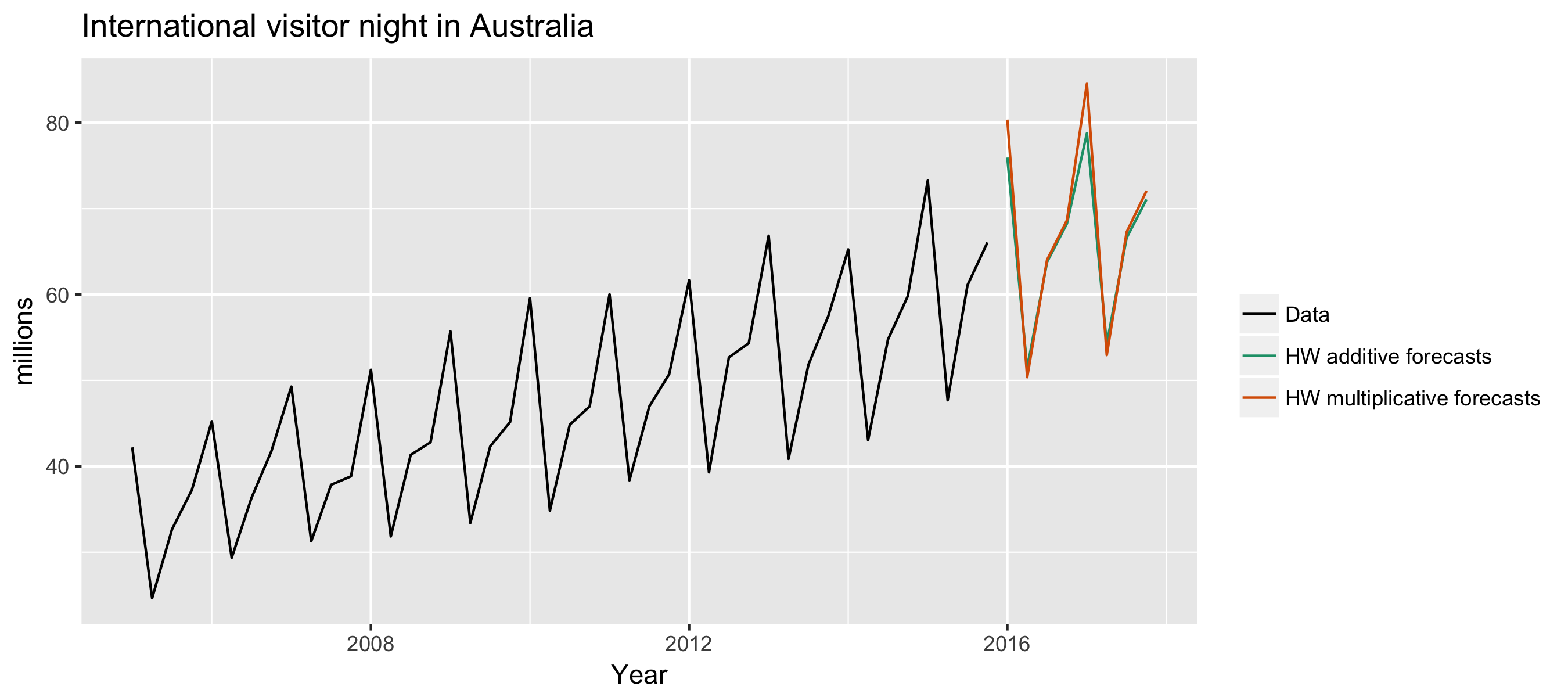
Example: Visitor Nights

aust <- window(austourists, start = 2005)
fc1  <- hw(aust, seasonal = "additive")
fc2  <- hw(aust, seasonal = "multiplicative")

ch3_vid3_visitor.png

Forecasting in R

Taxonomy of exponential smoothing methods

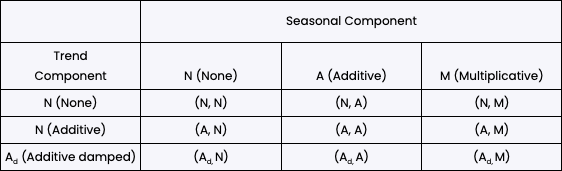
Taxonomy of exponential smoothing methods: trend and seasonal components

Forecasting in R

Taxonomy of exponential smoothing methods

Taxonomy of exponential smoothing methods: trend and seasonal components   Taxonomy of exponential smoothing methods: functions

Forecasting in R

Let's practice!

Forecasting in R

Preparing Video For Download...