Exponential smoothing methods with trend and seasonality
Forecasting in R

Rob J. Hyndman
Professor of Statistics at Monash University
Holt-Winters' additive method
| Holt-Winters additive method |
|---|
| $\hat{y}_{t+h \mid t} = \ell_t + hb_t + s_{t-m+h_m^+}$ |
| $\ell_t = \alpha(y_t - s_{t-m} )+ (1-\alpha)(\ell_{t-1} + b_{t-1})$ |
| $b_t = \beta^*(\ell_t = \ell_{t-1}) + (1 - \beta^*) b_{t-1}$ |
| $s_t = \gamma(y_t - \ell_{t-1} - b_{t-1}) + (1 - \gamma)s_{t-m}$ |
$s_{t-m+h_m^+}$ = seasonal component from final year of data
Smoothing parameters: $0 \leq \alpha \leq 1, \ 0 \leq \beta^* \leq 1, \ 0 \leq \gamma \leq 1 - \alpha$
$m$ = period of seasonality (e.g. $m = 4$ for quarterly data)
Seasonal component averages zero
Holt-Winters' multiplicative method
| Holt-Winters multiplicative method |
|---|
| $\hat{y}_{t+h \mid t} = (\ell_t + hb_t)s_{t-m+h_m^+}$ |
| $\ell_t = \alpha(\frac{y_t}{s_{t-m}} )+ (1-\alpha)(\ell_{t-1} + b_{t-1})$ |
| $b_t = \beta^*(\ell_t = \ell_{t-1}) + (1 - \beta^*) b_{t-1}$ |
| $s_t = \gamma\frac{y_t}{\ell_{t-1} - b_{t-1}} + (1 - \gamma)s_{t-m}$ |
- Seasonal component averages one
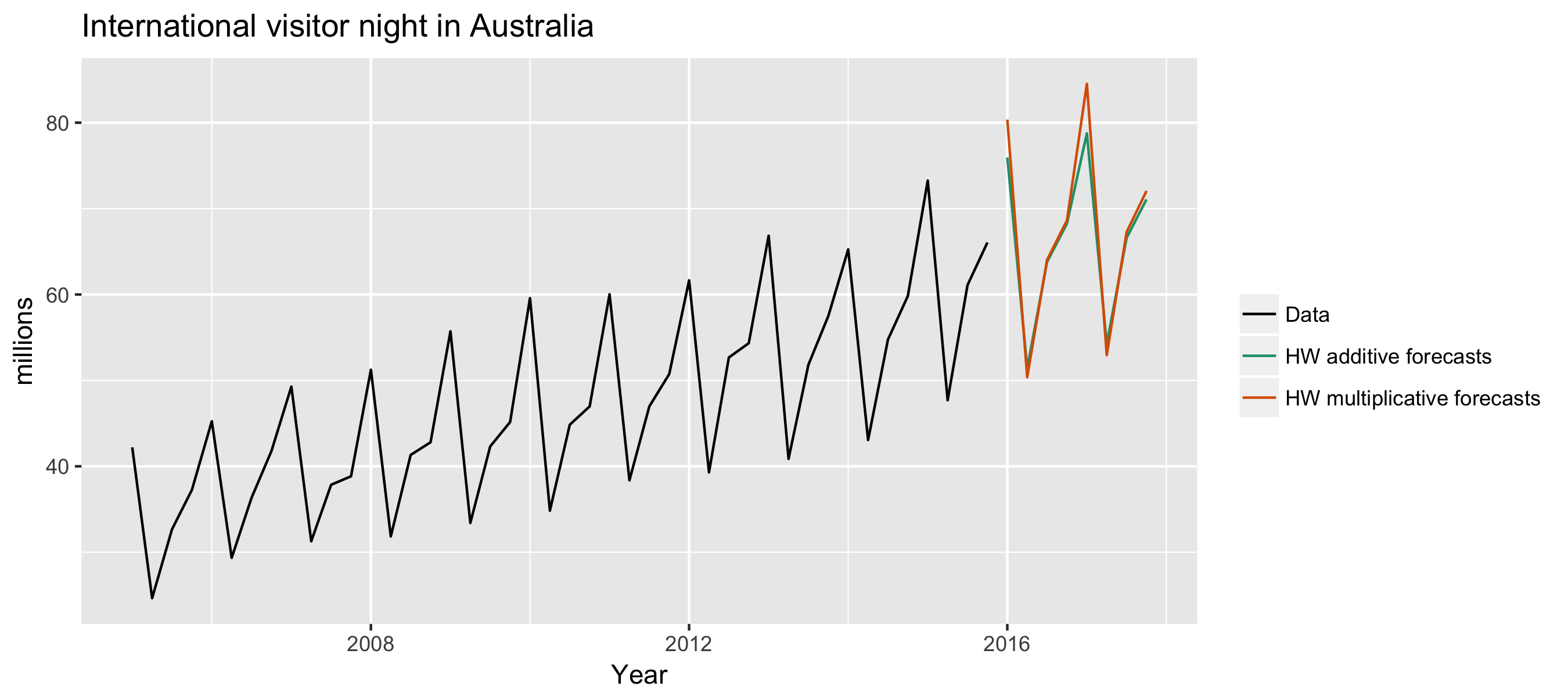
Example: Visitor Nights
aust <- window(austourists, start = 2005)
fc1 <- hw(aust, seasonal = "additive")
fc2 <- hw(aust, seasonal = "multiplicative")
Taxonomy of exponential smoothing methods
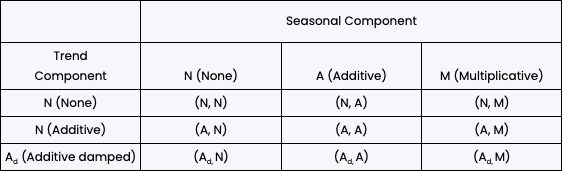
Taxonomy of exponential smoothing methods


Let's practice!
Forecasting in R

