Simulation ensembles: Monte-Carlo sampling

Discrete Event Simulation in Python

Diogo Costa (PhD, MSc)

Adjunct Professor, University of Saskatchewan, Canada & CEO of ImpactBLUE-Scientific

System response to different scenarios

Non-deterministic processes cause variation in system response
Previous video: Learned how to model non-deterministic processes
Characterize uncertainty propagation in model
Study system's response to different scenarios

This can assist with

Planning business expansions
Performing stress tests
Preparing for extreme situations

Monte Carlo sampling

Repeated random sampling
Model system with small changes
Examine system response to change

Parameter space as samples increase

Plot showing the results of 100 Monte Carlo samples. The model results' patterns are not visible.

Plot showing the results of 1500 Monte Carlo samples. Some model results' patterns are now visible but still limited.

Plot showing the results of 5000 Monte Carlo samples. The model results now show clear patterns, displaying a grid structure.

Monte Carlo sampling: Process investigation

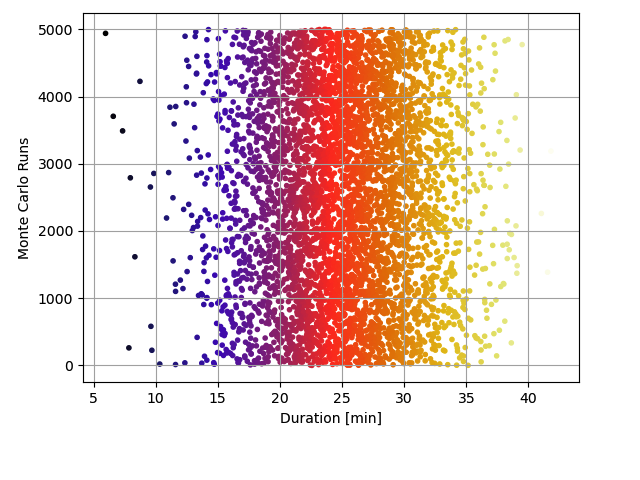
Example: Monte Carlo run to understand range of outputs of an event generator based on normal (gauss) distribution

import random as rd
import matplotlib.pyplot as plt

# Generating samples: Gaussian distribution
duration_sample = [rd.gauss(25, 5) 
for i in range(5000)]

# Plotting
plt.scatter(duration_sample, np.r_[0:5000], 
marker='.', c=duration_sample, cmap='CMRmap')

plt.xlabel("Duration [min]")
plt.ylabel("Monte Carlo Runs")

Plotting results Plot displaying Monte-Carlo sampling for durations generated based on the Gaussian Distribution.

Monte Carlo sampling: Discrete-event models

Underlying objective

Explore model uncertainty
Arising from non-deterministic processes
Characterize uncertainty
Support decision-making

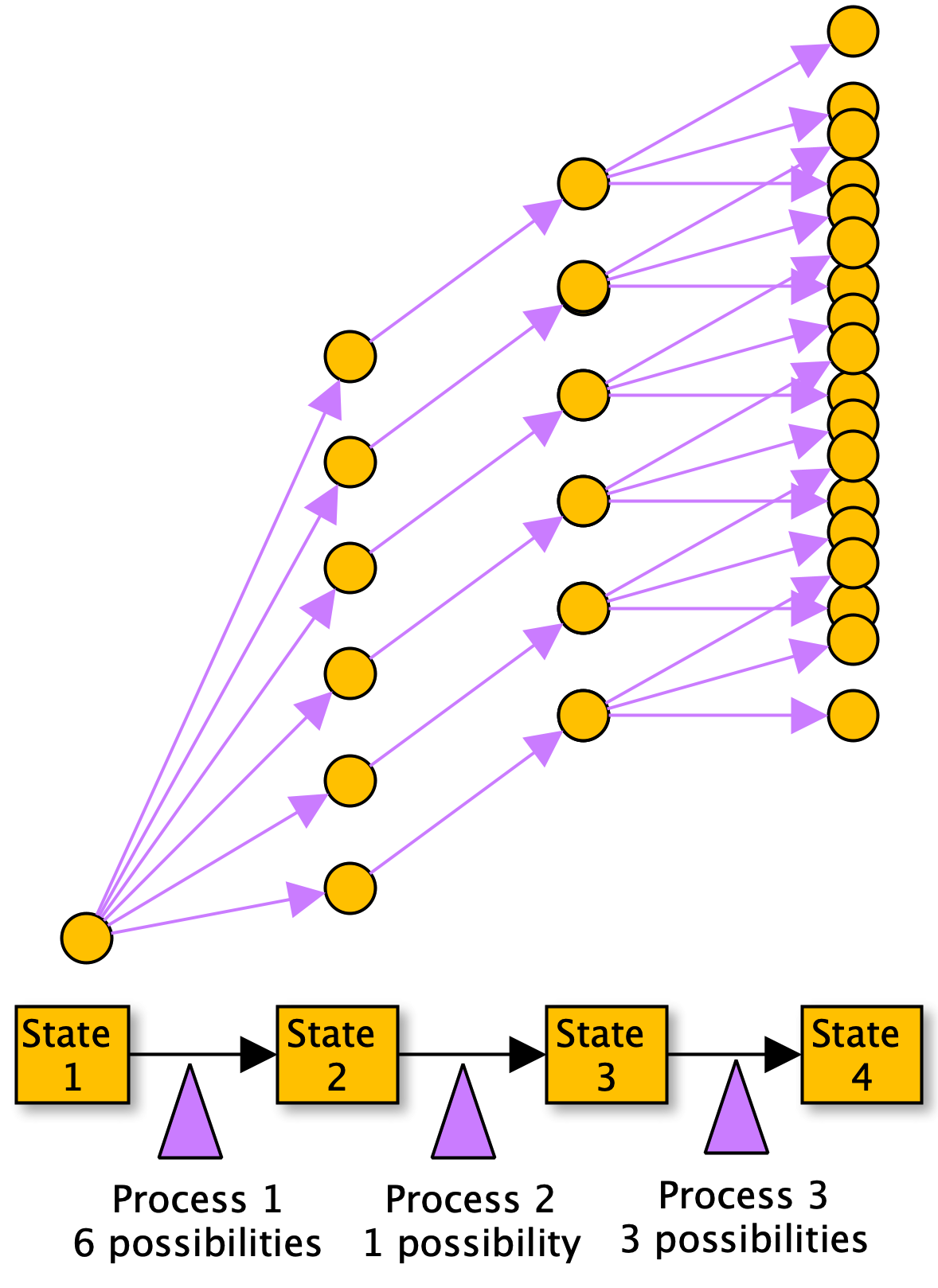
Diagram showing a system with four states, where processes change the states. Because there is variability in the duration of each process every time it repeats, the number of possibilities of the model system states increases through the sequence of processes.

Monte Carlo sampling: Discrete-event models

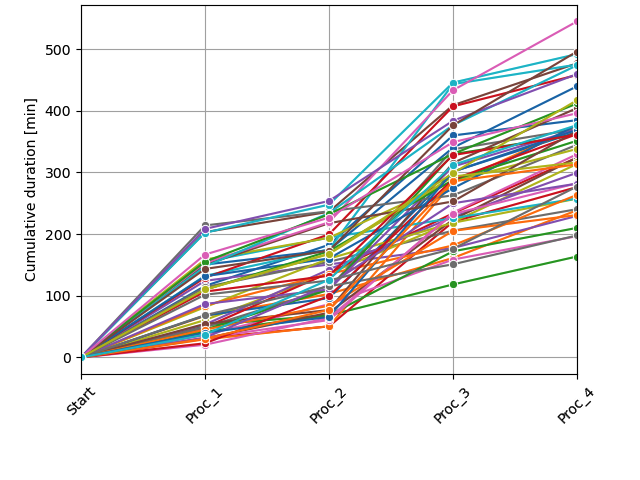
Uncertainty in each process duration propagates through system
Results in different model trajectories
Referred to as Response Envelope

Example:

n_trajectories = 50

process_1 = {"Name": "Raw_material", 
             "OperationTime": 20, 
             "MaxDelayTimePercent": 10}

process_2 = {"Name": "Unloading", 
            "OperationTime": 15, 
            "MaxDelayTimePercent": 5}

Plot showing the response envelope of a manufacturing activity that includes a series of sequential processes.

Let's practice!

Discrete Event Simulation in Python