Multiple comparisons tests

A/B Testing in Python

Moe Lotfy, PhD

Principal Data Science Manager

Introduction to the multiple comparisons problem

Single comparison:
- Control (A) versus Treatment (B)
- One metric
- No subcategories

Bar chart of average sales for two variants.

Multiple comparisons:
- Multiple variants (A/B/n tests)
- Multiple metrics
- Granular categories

Two bar charts with multiple variants and metrics.

Family-wise error rate

P(making Type I error) = $\alpha$ = 0.05
P(not making Type I error) = 1 - $\alpha$
P(not making Type I error in m tests) = (1 - $\alpha$)$^m$
P(making at least one Type I error in m tests) = 1 - (1 - $\alpha$)$^m$ = FWER

Family-wise Error Rate (FWER): the probability of making one or more type I errors when performing multiple hypothesis tests.

For a single test, FWER = 1 - (1 - $\alpha$)^1 = $\alpha$ = 0.05
But what if we perform more than one test?

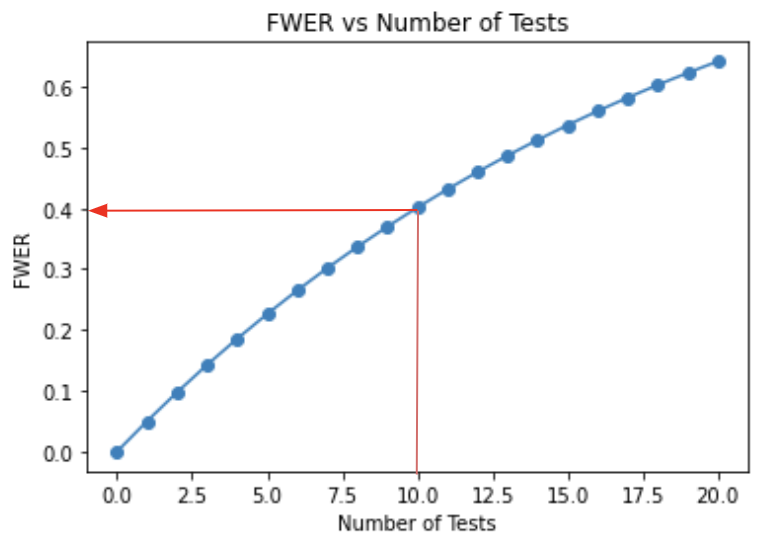
Family-wise error rate

import matplotlib.pyplot as plt 
import numpy as np 
alpha = 0.05 
x = np.linspace(0, 20, 21) 
y = 1-(1-alpha)**x 
plt.plot(x,y, marker='o') 
plt.title('FWER vs Number of Tests') 
plt.xlabel('Number of Tests') 
plt.ylabel('FWER') 
plt.show()

FWER = 1 - (1 - $\alpha$)^10
FWER for 10 tests = 40%

Line plot of FWER as a function of number of tests. FWER rises as number of tests increase.

Correction methods

The simplest and most popular approach is the Bonferroni Correction
Set the adjusted $\alpha$* to the individual test $\alpha$ divided by the number of tests m

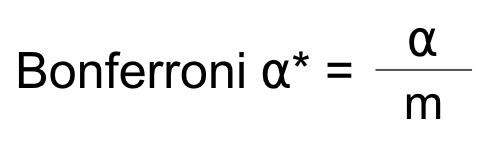
Bonferroni correction equation. Alpha divided by the number of comparisons 'm'

Less stringent Sidak correction
Set FWER to desired $\alpha$, then solve for $\alpha_s$

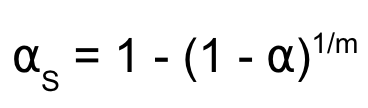
Sidak correction equation

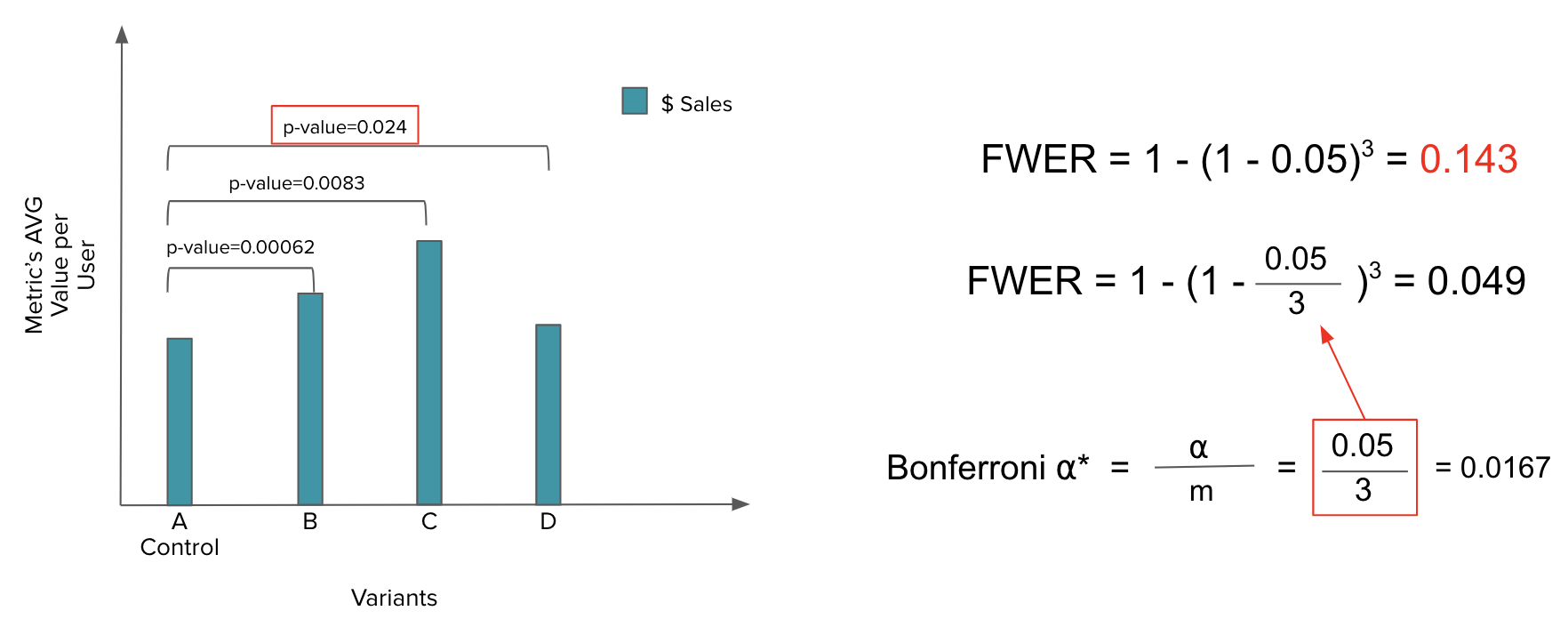
Bonferroni correction example

Without correction, all three tests are considered significant
- but the probability of making a type I error is inflated at 14%
With a Bonferroni Correction, A versus D is no longer significant, but FWER is controlled at 0.049

Bar chart of average sales for 4 variants with p-values.

statsmodels multipletests method

import statsmodels.stats.multitest as smt 
pvals = [0.023,0.0005,0.00004]

corrected = smt.multipletests(pvals, alpha=0.05, method='bonferroni')

print("Significant Test:", corrected[0])
print("Corrected P-values:", corrected[1])
print("Bonferroni Corrected alpha: {:.4f}".format(corrected[3]))

Significant Test: [False  True  True]
Corrected P-values: [0.069   0.0015  0.00012]
Bonferroni Corrected alpha: 0.0167

Let's practice!

A/B Testing in Python