Using derivatives to update model parameters

Introduction to Deep Learning with PyTorch

Jasmin Ludolf

Senior Data Science Content Developer, DataCamp

An analogy for derivatives

Derivative represents the slope of the curve

Steep slopes (red arrows):
- Large steps, derivative is high
Gentler slopes (green arrows):
- Small steps, derivative is low
Valley floor (blue arrow):
- Flat, derivative is zero

an image of a valley

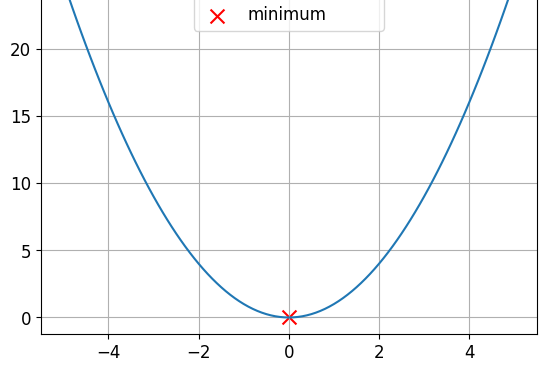
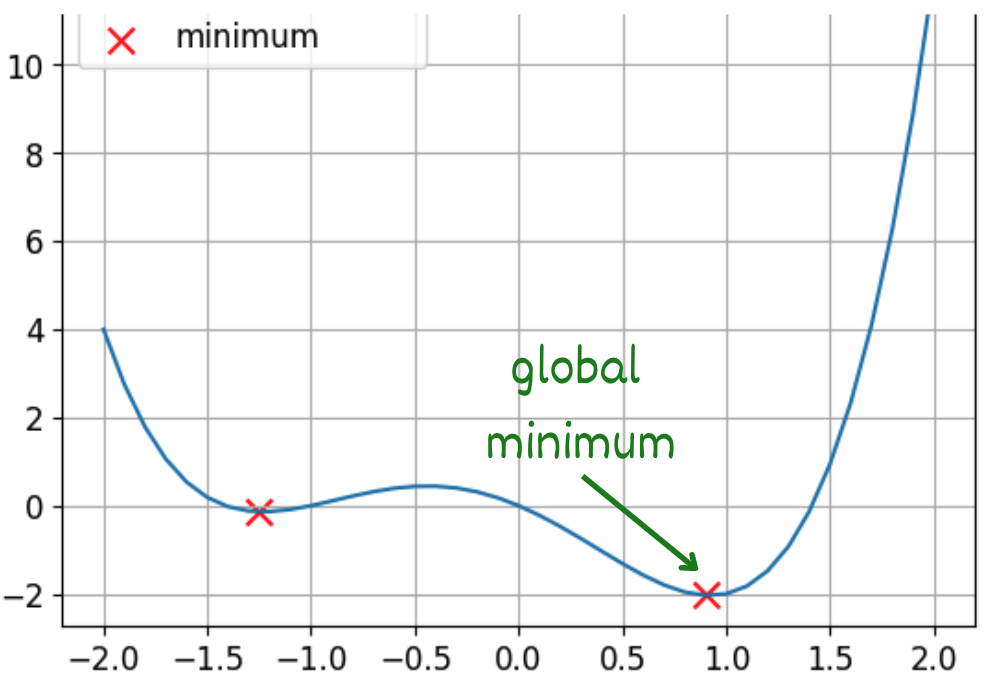
Convex and non-convex functions

This is a convex function

an example of convex function

This is a non-convex function

an example of non-convex function with global minimum highlighted

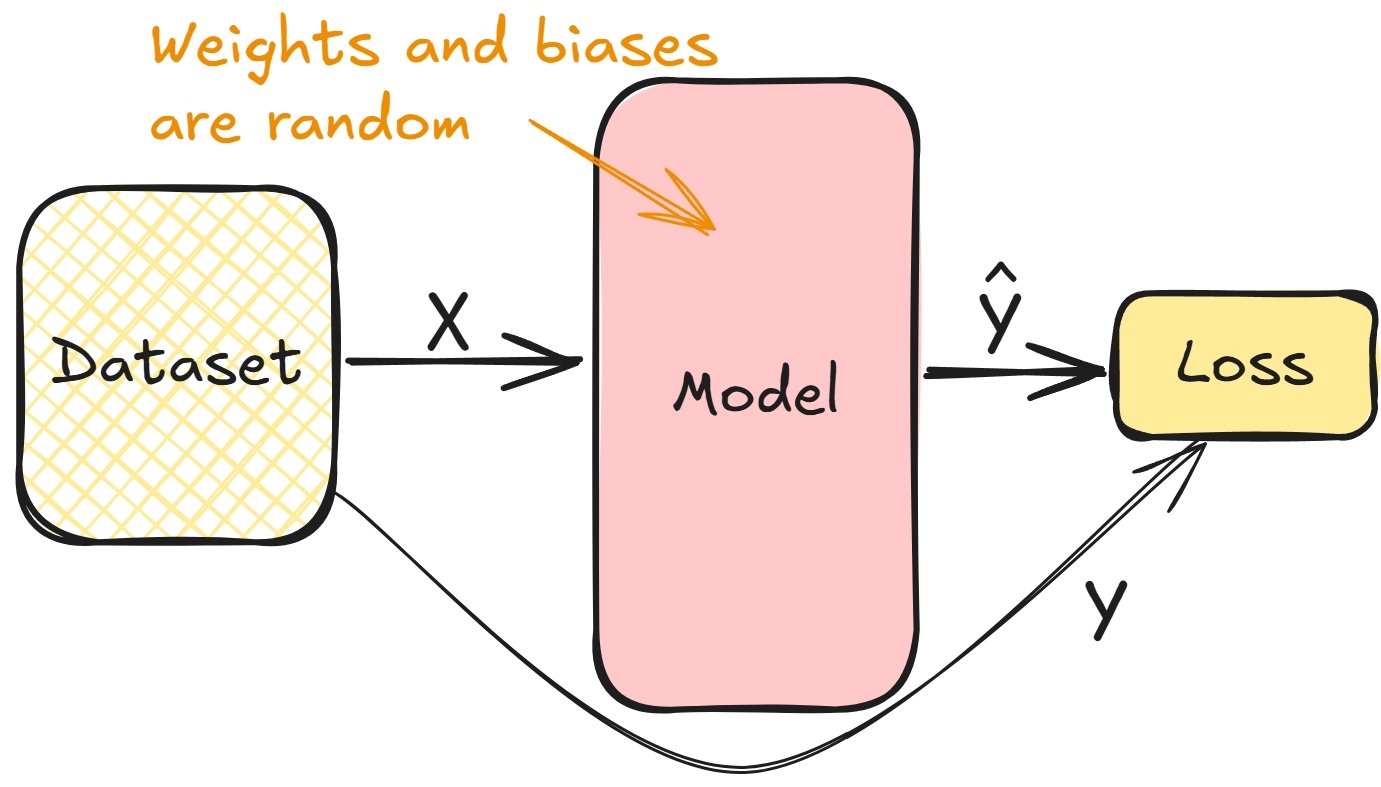
Connecting derivatives and model training

Compute the loss in the forward pass during training

$$ Calculating loss

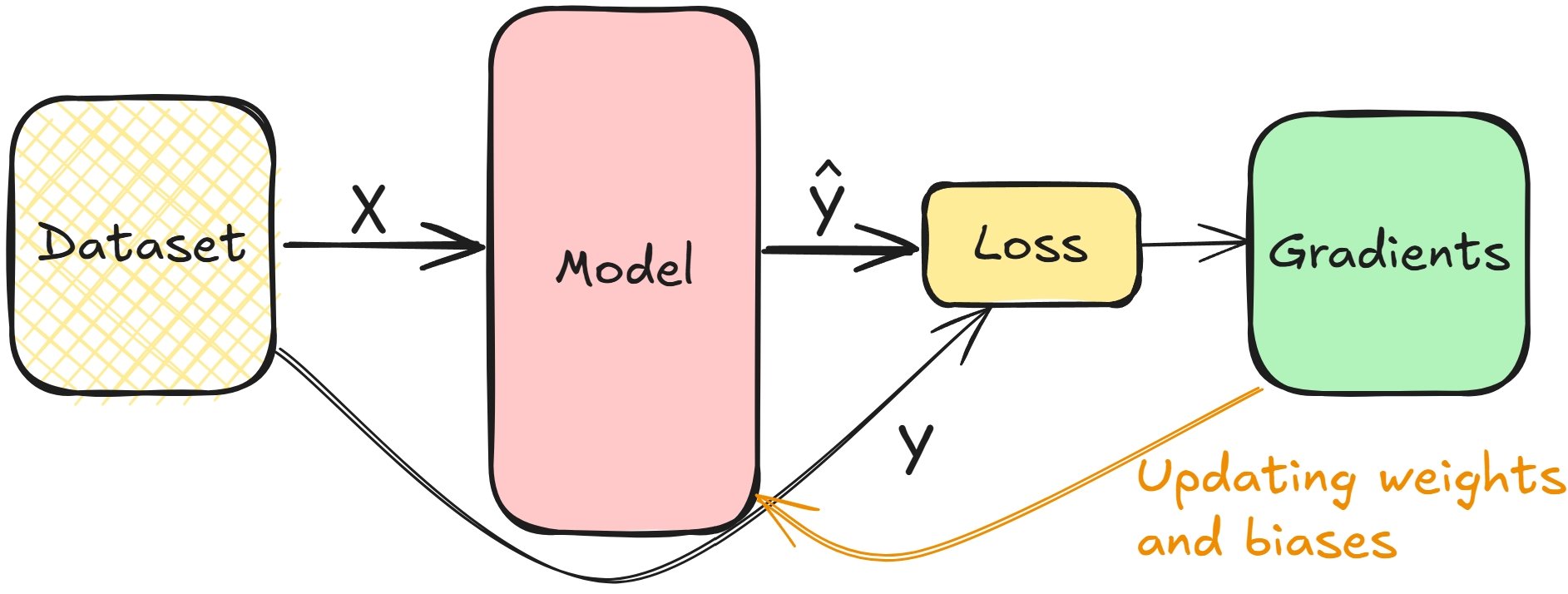
Connecting derivatives and model training

Gradients help minimize loss, tune layer weights and biases
Repeat until the layers are tuned

$$ Computing gradients

Backpropagation concepts

Consider a network made of three layers:
- Begin with loss gradients for $L2$
- Use $L2$ to compute $L1$ gradients
- Repeat for all layers ($L1$, $L0$)

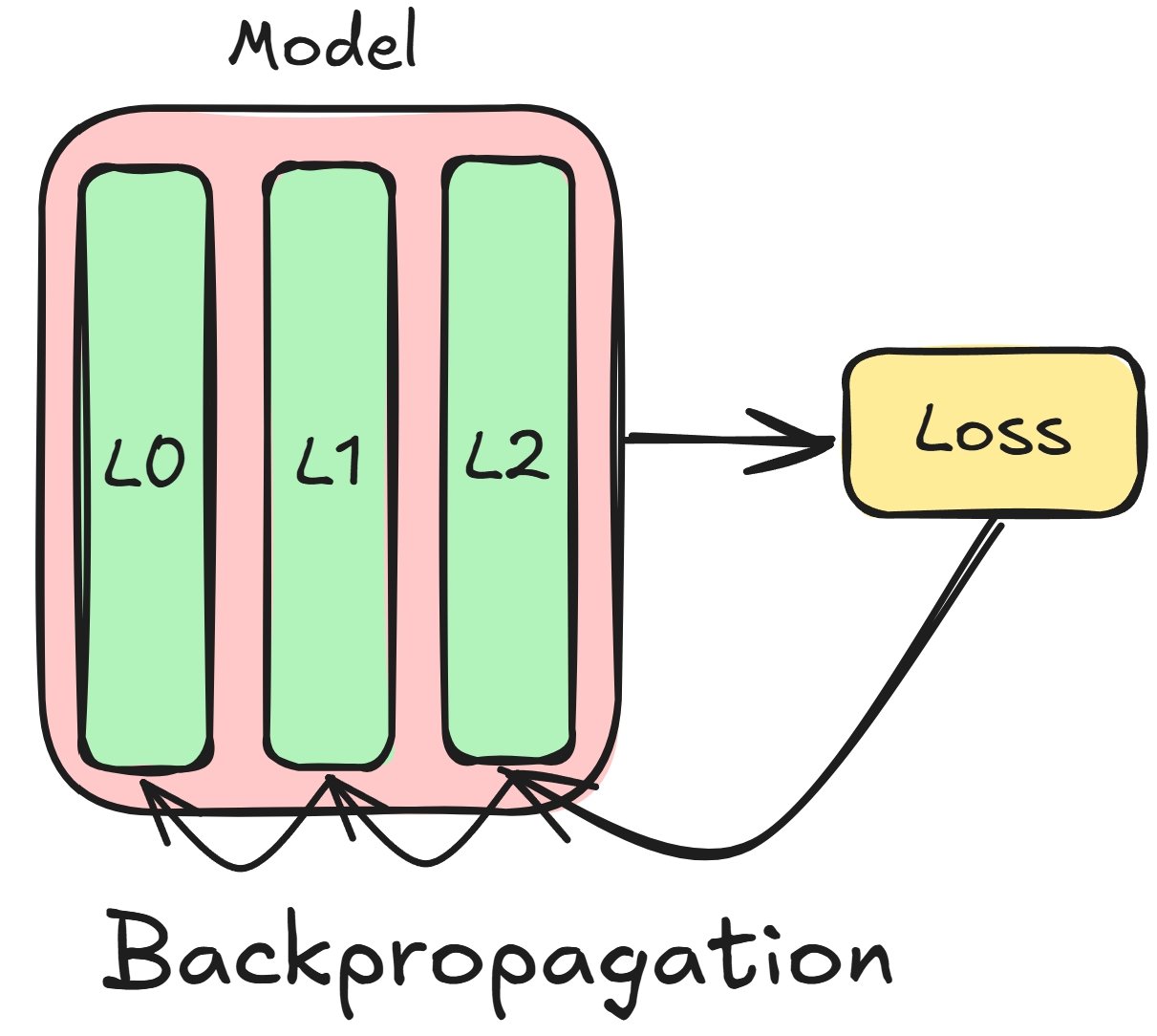
Backpropagation diagram

Backpropagation in PyTorch

# Run a forward pass 
model = nn.Sequential(nn.Linear(16, 8),
                      nn.Linear(8, 4),
                      nn.Linear(4, 2))
prediction = model(sample)


# Calculate the loss and gradients
criterion = CrossEntropyLoss()
loss = criterion(prediction, target)
loss.backward()

# Access each layer's gradients
model[0].weight.grad
model[0].bias.grad
model[1].weight.grad
model[1].bias.grad
model[2].weight.grad
model[2].bias.grad

Updating model parameters manually

# Learning rate is typically small
lr = 0.001

# Update the weights
weight = model[0].weight
weight_grad = model[0].weight.grad


weight = weight - lr * weight_grad


# Update the biases
bias = model[0].bias
bias_grad = model[0].bias.grad

bias = bias - lr * bias_grad

Access each layer gradient
Multiply by the learning rate
Subtract this product from the weight

Gradient descent

For non-convex functions, we will use gradient descent
PyTorch simplifies this with optimizers
- Stochastic gradient descent (SGD)

import torch.optim as optim

# Create the optimizer
optimizer = optim.SGD(model.parameters(), lr=0.001)


# Perform parameter updates
optimizer.step()

Let's practice!

Introduction to Deep Learning with PyTorch