Global optimization in SciPy

Introduction to Optimization in Python

Jasmin Ludolf

Content Developer

Global optimization

Production alternates between being expensive and cheap
- $\rightarrow$ $\Pi(q)$ has two distinct maxima at $5$ and $18$. Minimum is at $10$.

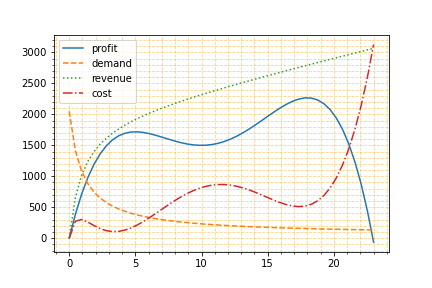
Demand, cost, revenue and profit vs quantity graph. Profit blue solid line, bimodal with 0s at 0 and 25, two maxima at 5 and 18 and a local minimum at 10

Getting stuck in a local optimum

from scipy.optimize import minimize_scalar, minimize


def profit(q):
  return -q**4 / 4 + 11 * q**3 - 160 * q**2 + 900 * q


result_min_scalar = minimize_scalar(lambda q: -profit(q))

print(f"{result_min_scalar.message}")
print(f"The maximum according to minimize_scalar is {-result_min_scalar.fun:.2f} \
and achieved at {result_min_scalar.x:.2f}\n")

Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
The maximum according to minimize_scalar is 1718.75 and achieved at 5.00

Getting stuck in a local optimum

x0 = 9
result = minimize(lambda q: -profit(q), x0, bounds=[(0, 20)])
print(f"{result.message}")
print(f"The maximum according to minimize(x0={x0}) is {-result.fun:.2f} at {result.x[0]:.2f}\n")

CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
The maximum according to minimize(x0=9) is 1718.75 at 5.00

x0 = 10 + 1e-8
result = minimize(lambda q: -profit(q), x0)
print(f"{result.message}")
print(f"The maximum according to minimize(x0={x0}) is {-result.fun:.2f} at {result.x[0]:.2f}\n")

Optimization terminated successfully.
The maximum according to minimize(x0=10.00000001) is 1500.00 at 10.00

Getting unstuck with basinhopping

from scipy.optimize import basinhopping


x0 = 0
result = basinhopping(lambda q: -profit(q), x0, niter=10000)


print(f"{result.message}")
print(f"The maximum according to basinhopping(x0={x0}, niter=10000) \
is {-result.fun:.2f} at {result.x[0]:.2f}\n")

['requested number of basinhopping iterations completed successfully']
The maximum according to basinhopping(x0=0, niter=10000) is 2268.00 at 18.00

basinhopping with kwargs and bounds

from scipy.optimize import basinhopping, NonlinearConstraint

x0 = 0
kwargs = {"constraints": NonlinearConstraint(lambda x: x, lb=0, ub=30)}


result = basinhopping(lambda q: -profit(q), x0, minimizer_kwargs=kwargs)
print(f"{result.message}")
print(f"The maximum according to basinhopping(x0={x0}) is at {result.x[0]:.2f}\n")

['requested number of basinhopping iterations completed successfully']
The maximum according to basinhopping(x0=0) is at 18.00

basinhopping with callback

from scipy.optimize import basinhopping, LinearConstraint

x0 = 0
kwargs = {"constraints": LinearConstraint([1], lb=0, ub=30)} 


maxima = []

def callback(x, f, accept):
    if accept:
        maxima.append(*x)


result = basinhopping(lambda q: -profit(q), 
                      x0,
                      callback=callback,
                      minimizer_kwargs=kwargs,
                      niter=5)

basinhopping - callback output

print(f"{result.message}")
print(f"The maximum according to basinhopping(x0={x0}) is at {result.x[0]:.2f}\n")
print(f"(Local) maxima found by basinhopping are: {[round(x, 2) for x in maxima]}")

$$ $$

['requested number of basinhopping iterations completed successfully']
The maximum according to basinhopping(x0=0) is at 18.00 
(Local) maxima found by basinhopping are: [5.0, 5.0, 5.0, 5.0, 5.0, 18.0]

Set seed argument to replicate results

Let's practice!

Introduction to Optimization in Python