Convex-constrained optimization with inequality constraints

Introduction to Optimization in Python

Jasmin Ludolf

Content Developer

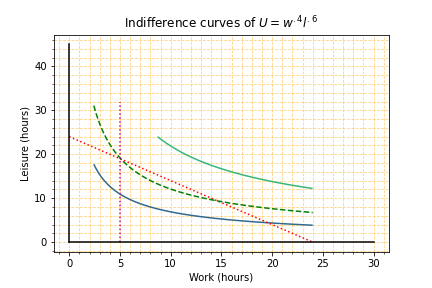
Corner versus interior solution

  • Alexia only has 5 hours worth of work

$$ w\leq 5$$

  • Two constraints:
    • 24 hours in a day
    • 5 hours of work
  • The constraints form a corner
  • Interior solution is not an intersection

Indifference curves and constraints. The indifference curve at optimal utility level passes through the intersection of constraints.

Introduction to Optimization in Python

Manufacturer with capacity constraints

  • Automaker produces identical cars in two plants $A$, $B$
    • Quantities: $q_A$, $q_B$
    • Capacity: $q_A\leq 90$, $q_B\leq 90$
    • Cost: $C_A(q)=3q$, $C_B(q)=3.5q$
  • Demand:
    • $P=120-Q$
  • Contract:
    • $Q\geq 92$
  • Objective to maximize profit:
    • $\displaystyle\max \Pi(q_A,q_B)$

Car manufacturing line

Introduction to Optimization in Python

Maximizing profit

  • Objective:
    • $\Pi = R-C$
      • $R = PQ$
Introduction to Optimization in Python

Maximizing profit

  • Objective:
    • $\Pi = R-C$
      • $R = PQ = (120-Q)Q $
Introduction to Optimization in Python

Maximizing profit

  • Objective:

    • $\Pi = R-C$
      • $R = PQ = (120-Q)Q=\left[120-(q_A+q_B)\right](q_A+q_B)$
      • $C=C_A+C_B=3q_A+3.5q_B$

  • Bounds

    • $0\leq q_A, q_B\leq 90$
  • Constraints
    • $Q\geq92\Leftrightarrow 92\leq q_A+q_B$
Introduction to Optimization in Python

Formulation

$$\max_{q_A,q_B}R(q_A,q_B)-C(q_A,q_B)$$

$$s.t.$$

$$R(q_A,q_B)=\left[120-(q_A+q_B)\right](q_A+q_B)$$

$$\ \ \ \ \ C(q_A,q_B)=3q_A+3.5q_B$$

$$\ \ \ 0\leq q_A, q_B\leq 90$$

$$ \ \ \ \ 92\leq q_A+q_B$$

from scipy.optimize import minimize,\
        Bounds, LinearConstraint


def R(q):
    return (120 - (q[0] + q[1]
       )) * (q[0] + q[1])

def C(q): return 3*q[0] + 3.5*q[1] 

def profit(q): return R(q) - C(q)


bounds = Bounds([0, 0], [90, 90])


constraints = LinearConstraint([1, 1], 
                               lb=92)
Introduction to Optimization in Python

Maximize profit with SciPy

result = minimize(lambda q: -profit(q),

                  [50, 50],

                  bounds=bounds,
                  constraints=constraints)

print(result.message)
print(f'The optimal number of cars produced in plant A is: {result.x[0]:.2f}')
print(f'The optimal number of cars produced in plant B is: {result.x[1]:.2f}')
print(f'The firm made: ${-result.fun:.2f}')

Optimization terminated successfully
The optimal number of cars produced in plant A is: 90.00
The optimal number of cars produced in plant B is: 2.00
The firm made: $2299.00
Introduction to Optimization in Python

Non-linear contraints in SciPy

from scipy.optimize import NonlinearConstraint 
import numpy as np


constraints = NonlinearConstraint(lambda q: q[0] + q[1], lb=92, ub=np.Inf)


result = minimize(lambda q: -profit(q), 
                  [50, 50], 
                  bounds=Bounds([0, 0], [90, 90]),
                  constraints=constraints)
Introduction to Optimization in Python

Solution with NonlinearConstraint

print(result.message)
print(f'The optimal number of cars produced in plant A is: {result.x[0]:.2f}')
print(f'The optimal number of cars produced in plant B is: {result.x[1]:.2f}')
print(f'The firm made: ${-result.fun:.2f}') 

Optimization terminated successfully
The optimal number of cars produced in plant A is: 90.00
The optimal number of cars produced in plant B is: 2.00
The firm made: $2299.00
  • Use LinearConstraint() for straightforward, linear problems
  • Otherwise, use NonlinearConstraint()
Introduction to Optimization in Python

Let's practice!

Introduction to Optimization in Python

Preparing Video For Download...