Multivariate optimization

Introduction to Optimization in Python

Jasmin Ludolf

Content Developer

The biscuit factory

 

Objective function:

  • $F = K^{0.34} \times L^{0.66}$
    • $F$: production function
    • Labor ($L$): hours put in by workers
    • Capital ($K$): hours machines operated
    • Multivariate problem

 

Biscuits on a production line.

Introduction to Optimization in Python

Partial derivatives

 

Univariate

 

Objective function:

$p = 40q - 0.5q^2$

Derivative: slope of the objective function changes with changes to single variable

$\frac{dp}{dq} = 40 - q$

 

Multivariate

 

Objective function:

$F = K^{0.34} \times L^{0.66}$

Partial derivatives: how the slope changes with respect to each variable

$\frac{\partial F}{\partial K}$ and $\frac{\partial F}{\partial L}$

Introduction to Optimization in Python

Solving multivariate problems

 

Objective function:

  • $F = K^{0.34} \times L^{0.66}$
    • $F$: production function
    • Labor ($L$): hours put in by workers
    • Capital ($K$): hours machines operated
from sympy import symbols, diff, solve


K, L = symbols('K L')
F = K**.34 * L**.66


dF_dK = diff(F, K)
dF_dL = diff(F, L)

crit_points = solve([dF_dK, dF_dL], (K, L))


print(crit_points)

[]
Introduction to Optimization in Python

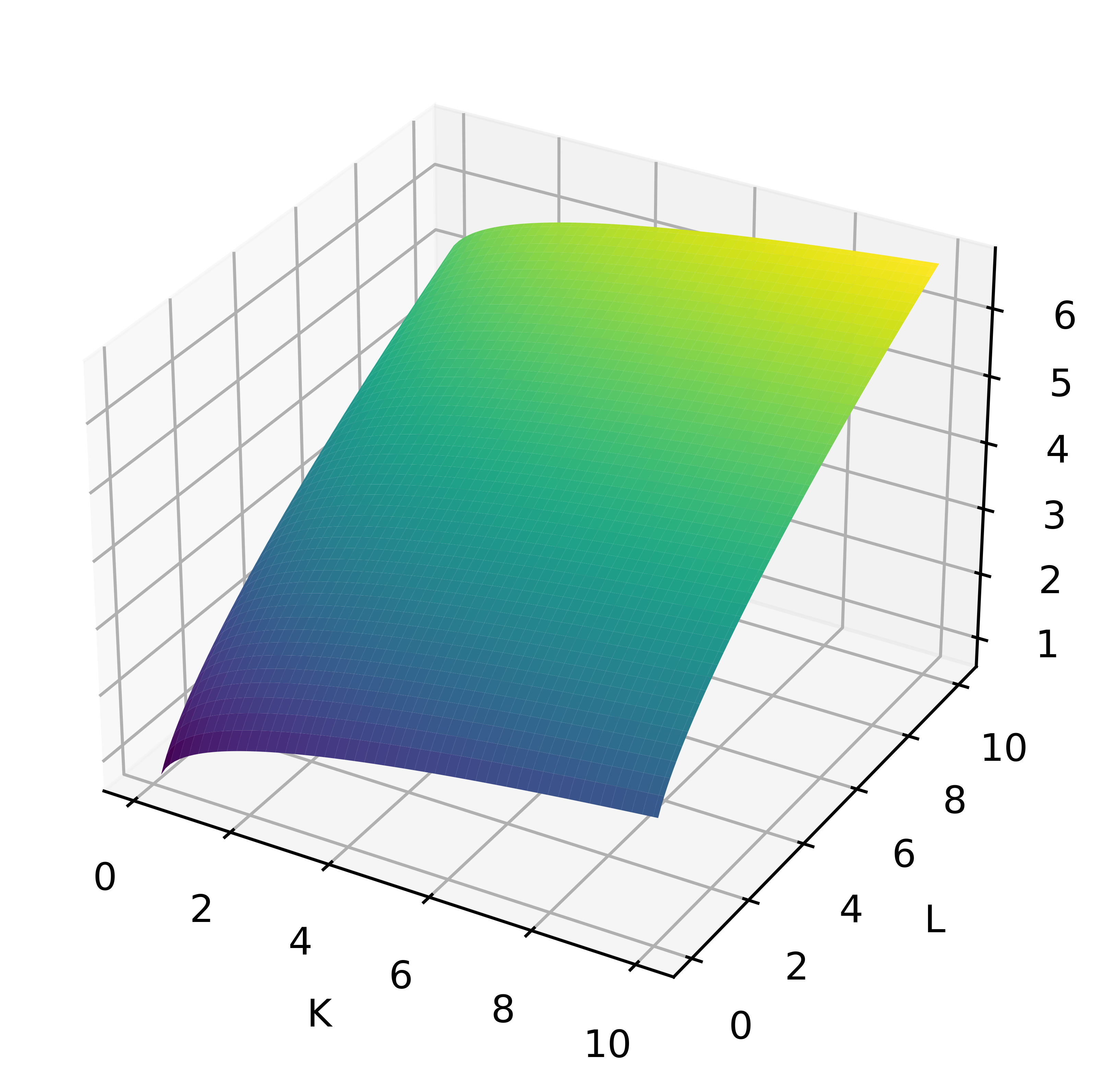
Our production function

 

Objective function:

  • $F = K^{0.34} \times L^{0.66}$
  • As $K$ and $L$ increase, $F$ increases
  • No maxima or minima!

A 3D plot of the biscuit production function.

Introduction to Optimization in Python

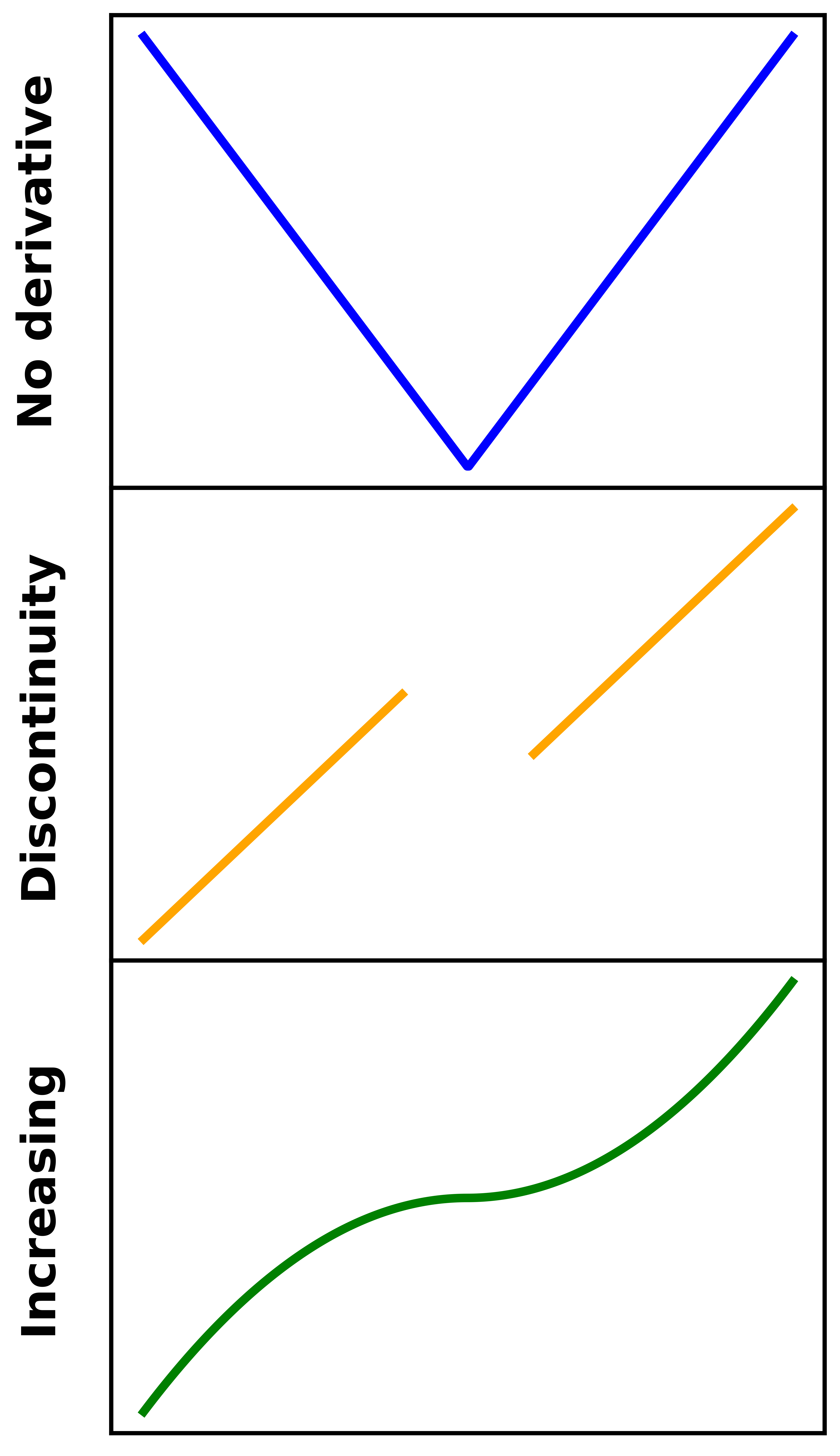
The limits of differentiation

 

Watch out for:

  • No derivative
  • Discontinuities
  • Increasing or decreasing functions

 

  • Non-differentiable: cannot be optimized using differentiation

Three plots of functions where differentiation wouldn't be able to find the maxima or minima.

Introduction to Optimization in Python

Let's practice!

Introduction to Optimization in Python

Preparing Video For Download...